 και
και  είναι οι προβολές των
είναι οι προβολές των  και
και  σε μεταβλητή ευθεία
σε μεταβλητή ευθεία  , η οποία
, η οποία διέρχεται από την αρχή των αξόνων . Βρείτε τον γεωμετρικό τόπο του μέσου
 , του τμήματος
, του τμήματος  .
.Συντονιστής: Τηλέγραφος Κώστας
 και
και  είναι οι προβολές των
είναι οι προβολές των  και
και  σε μεταβλητή ευθεία
σε μεταβλητή ευθεία  , η οποία
, η οποία  , του τμήματος
, του τμήματος  .
.Έστω


 και επειδή
και επειδή  καταλήγουμε ότι ο γεωμετρικός τόπος είναι κύκλος
καταλήγουμε ότι ο γεωμετρικός τόπος είναι κύκλος  που διέρχεται από την αρχή των αξόνων και από τα σημεία
που διέρχεται από την αρχή των αξόνων και από τα σημεία 
 είναι κατακόρυφη, το μέσο του
είναι κατακόρυφη, το μέσο του  είναι
είναι 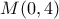 που ανήκει στον παραπάνω κύκλο.
που ανήκει στον παραπάνω κύκλο. είναι σταθερά . το μέσο
είναι σταθερά . το μέσο  του
του  σταθερό και το
σταθερό και το  ενώνει
ενώνει  και άρα
και άρα  .
. ανήκει στον κύκλο διαμέτρου
ανήκει στον κύκλο διαμέτρου 
 σημείο του τόπου και
σημείο του τόπου και  , Με
, Με  θα ισχύουν:
θα ισχύουν: 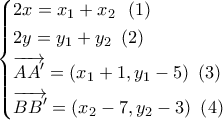
 είναι κάθετο στα δυανύσματα που εκφράζουν οι
είναι κάθετο στα δυανύσματα που εκφράζουν οι  .
.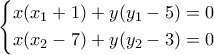 και προσθέτω κατά μέλη:
και προσθέτω κατά μέλη:  . κύκλος κ.λ.π.
. κύκλος κ.λ.π.Μέλη σε αυτήν τη Δ. Συζήτηση: MSN [Bot] και 2 επισκέπτες