 Ευθύγραμμο τμήμα
Ευθύγραμμο τμήμα  έχει τα άκρα του στις ευθείες
έχει τα άκρα του στις ευθείες  και
και 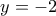 αντίστοιχα και διέρχεται από
αντίστοιχα και διέρχεται από την αρχή των αξόνων . Από το σημείο
 φέρω τμήμα :
φέρω τμήμα :  .
. α) Βρείτε τον γεωμετρικό τόπο του σημείου
 . β) Βρείτε τη θέση του
. β) Βρείτε τη θέση του  , ώστε να είναι
, ώστε να είναι  .
.Συντονιστής: Τηλέγραφος Κώστας
 Ευθύγραμμο τμήμα
Ευθύγραμμο τμήμα  έχει τα άκρα του στις ευθείες
έχει τα άκρα του στις ευθείες  και
και 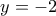 αντίστοιχα και διέρχεται από
αντίστοιχα και διέρχεται από  φέρω τμήμα :
φέρω τμήμα :  .
.  . β) Βρείτε τη θέση του
. β) Βρείτε τη θέση του  , ώστε να είναι
, ώστε να είναι  .
.Κάπως πιο γενικά (για το α):
 ανήκει σε κύκλο διαμέτρου
ανήκει σε κύκλο διαμέτρου  , άρα οι εξισώσεις των ευθειών στις οποίες ανήκουν τα
, άρα οι εξισώσεις των ευθειών στις οποίες ανήκουν τα  ,
,  είναι περιττές (όσον αφορά αυτό το ερώτημα).
είναι περιττές (όσον αφορά αυτό το ερώτημα). έχει συντεταγμένες
έχει συντεταγμένες  , τότε το κέντρο του κύκλου
, τότε το κέντρο του κύκλου  θα έχει συντεταγμένες
θα έχει συντεταγμένες  και επιπλέον:
και επιπλέον:

 ,
, 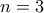 , η εξίσωση γράφεται
, η εξίσωση γράφεται  .
. , θα είναι
, θα είναι  αν και μόνο αν
αν και μόνο αν  .
. , τότε
, τότε  , ενώ επίσης:
, ενώ επίσης:
 είναι ορθογώνιο όταν
είναι ορθογώνιο όταν  και
και  ή
ή  και
και  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: MSN [Bot] και 2 επισκέπτες