Καλησπέρα σε όλους. Η προσπάθεια με Αναλυτική και μελέτη συναρτήσεων οδηγεί σε πολύπλοκη συνάρτηση. To λογισμικό δείχνει ελάχιστο εκεί που το προσδιορίζουν ο
Θανάσης και ο
Νίκος.
Γεωμετρικά πιστεύω ότι κινούμαι στον ίδιο περίπου δρόμο (*) με τον
Νίκο (αν και κόβω δρόμο με την εξίσωση της

...
(*) Όταν το ανάρτησα ΔΕΝ είχα δει τη λύση του
Νίκου. Θα τη δω στη συνέχεια.

- 26-06-2018 Γεωμετρία.png (38.26 KiB) Προβλήθηκε 760 φορές
Έστω

το μέσο του

. Ο κύκλος με διάμετρο το

διέρχεται από το

.
To  (άρα και το
(άρα και το  ) θα γίνει ελάχιστο όταν ο κύκλος θα εφάπτεται στην
) θα γίνει ελάχιστο όταν ο κύκλος θα εφάπτεται στην  , στο
, στο  .
edit:
.
edit: Το

είναι μεταβλητό σημείο. Αν δεν αποδείξω την παραπάνω εικασία (...που προφανώς ισχύει) η απόδειξη
δεν μπορεί να θεωρηθεί πλήρης.
Οπότε

και το

είναι το μέσο του

, όπου

η προβολή του

στην

.
Έστω

.
Είναι

, οπότε

(2).
Έστω

, οπότε

Οπότε

.
edit: Τότε είναι

και

και καταλήγω (από άλλο δρόμο) στο αποτέλεσμα του
Νίκου.
Λύση με μελέτη συνάρτησης:
Έστω

.
Το τεταρτοκύκλιο έχει εξίσωση

(1)
Είναι

, οπότε

(2).
Λύνουμε το σύστημα των (1) και (2).
Έχουμε

, από όπου προκύπτει

(Σχετικά) εύκολα δείχνουμε ότι

και

για

Οπότε

.
Τότε


.
και συνεχίζει ... (;) ...
 κινείται στην ακτίνα
κινείται στην ακτίνα  , τεταρτοκυκλίου
, τεταρτοκυκλίου  . Η κάθετη
. Η κάθετη στο
στο  , τέμνει το τόξο στο
, τέμνει το τόξο στο  . Βρείτε το ελάχιστο του τμήματος
. Βρείτε το ελάχιστο του τμήματος  .
. και
και 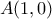 , βρείτε την τετμημένη
, βρείτε την τετμημένη  ,του σημείου
,του σημείου  .
. , τόσο μικρότερη θα είναι η υποτείνουσα ( γιατί ; )
, τόσο μικρότερη θα είναι η υποτείνουσα ( γιατί ; )
 και άρα το μήκος της υποτείνουσας
και άρα το μήκος της υποτείνουσας  .
.

 η προβολή του
η προβολή του  και
και  ρο μέσο της
ρο μέσο της  .
. 
 έχω :
έχω : 
 έχω :
έχω : 
 . Δηλαδή :
. Δηλαδή :  .
. είναι όμοια θα έχω :
είναι όμοια θα έχω :  (Με διανύσματα προκύπτει η ίδια με εσωτερικό γινόμενο.)
(Με διανύσματα προκύπτει η ίδια με εσωτερικό γινόμενο.) έχω :
έχω : 
 αλλά από το Π. Θ. στα
αλλά από το Π. Θ. στα 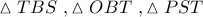 έχω :
έχω :
 δίδει :
δίδει :  ή λόγω της
ή λόγω της 
 έχω εκφράσει το
έχω εκφράσει το  με δύο τρόπους .
με δύο τρόπους . το
το  γίνεται
γίνεται  . Τότε όμως
. Τότε όμως  και εξισώνοντας τα δεύτερα μέλη
και εξισώνοντας τα δεύτερα μέλη  έχω :
έχω :  και άρα :
και άρα : επειδή δε λόγω της
επειδή δε λόγω της  είναι
είναι  βρίσκω:
βρίσκω: 
 με την
με την 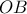
 το μέσο του
το μέσο του  . Ο κύκλος με διάμετρο το
. Ο κύκλος με διάμετρο το  (άρα και το
(άρα και το  και το
και το  , όπου
, όπου  η προβολή του
η προβολή του  .
.  , οπότε
, οπότε  (2).
(2).  , οπότε
, οπότε 
 .
. και
και  και καταλήγω (από άλλο δρόμο) στο αποτέλεσμα του
και καταλήγω (από άλλο δρόμο) στο αποτέλεσμα του  (1)
(1) , οπότε
, οπότε  (2).
(2).  , από όπου προκύπτει
, από όπου προκύπτει 
 και
και  για
για 
 .
.
 .
. τότε
τότε  . Έστω
. Έστω  .
.
 δηλαδή το
δηλαδή το  .
. η ελάχιστη τιμή του
η ελάχιστη τιμή του  είναι
είναι  , όταν το
, όταν το  είναι ανάμεσα στα
είναι ανάμεσα στα  και
και 