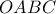 , έτσι ώστε η κορυφή
, έτσι ώστε η κορυφή  να συμπέσει με την
να συμπέσει με την  .
.Η νέα θέση της κορυφής
 είναι η
είναι η  , της οποίας να βρείτε τις συντεταγμένες .
, της οποίας να βρείτε τις συντεταγμένες .Συντονιστής: Τηλέγραφος Κώστας
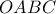 , έτσι ώστε η κορυφή
, έτσι ώστε η κορυφή  να συμπέσει με την
να συμπέσει με την  .
. είναι η
είναι η  , της οποίας να βρείτε τις συντεταγμένες .
, της οποίας να βρείτε τις συντεταγμένες .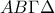 διαστάσεων
διαστάσεων  διπλώνεται κατά μήκος της ευθείας
διπλώνεται κατά μήκος της ευθείας  έτσι ώστε η κορυφή
έτσι ώστε η κορυφή  να συμπέσει με την
να συμπέσει με την  , όπως στην εικόνα. Πόσο είναι το εμβαδόν του τετραπλεύρου
, όπως στην εικόνα. Πόσο είναι το εμβαδόν του τετραπλεύρου  ;
; 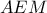 και
και  είναι ίσα ως ορθογώνια με
είναι ίσα ως ορθογώνια με  και, λόγω παραλληλίας των
και, λόγω παραλληλίας των  , έχουμε
, έχουμε  . Έτσι το
. Έτσι το  είναι ισεμβαδικό με το
είναι ισεμβαδικό με το  . Επίσης το
. Επίσης το  ισούται με το
ισούται με το  από το οποίο προέκυψε με την δίπλωση. Άρα τα ισεμβαδικά
από το οποίο προέκυψε με την δίπλωση. Άρα τα ισεμβαδικά  έχουν, το καθένα, εμβαδόν όσο το μισό του αρχικού ορθογωνίου παραλληλογράμμου, δηλαδή
έχουν, το καθένα, εμβαδόν όσο το μισό του αρχικού ορθογωνίου παραλληλογράμμου, δηλαδή  . Συμπεραίνουμε ότι και το ίσο τους
. Συμπεραίνουμε ότι και το ίσο τους  έχει εμβαδόν
έχει εμβαδόν  .
.
 . Αν
. Αν  θα είναι
θα είναι  . . Αλλά
. . Αλλά 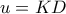 οπότε από το Π. Θ. στο
οπότε από το Π. Θ. στο  θα έχω:
θα έχω:  και άρα :
και άρα : 
 . Η κάθετη σ αυτή ευθεία
. Η κάθετη σ αυτή ευθεία 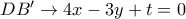 και αφού επαληθεύεται από το
και αφού επαληθεύεται από το  έχω:
έχω:  .
. Τώρα το
Τώρα το  θα προκύψει από την τομή της προηγουμένης ευθείας με την από το
θα προκύψει από την τομή της προηγουμένης ευθείας με την από το  παράλληλη στην ευθεία
παράλληλη στην ευθεία  ,
,  κάθετη στην
κάθετη στην  ) ( επιλέγω τη δεύτερη)
) ( επιλέγω τη δεύτερη) και η
και η  θα έχει εξίσωση :
θα έχει εξίσωση :  Το σύστημα των
Το σύστημα των  δίδει:
δίδει: 
ΤοMihalis_Lambrou έγραψε: ↑Παρ Δεκ 28, 2018 1:23 amΜικρή παραλλαγή της είχε πέσει στον Διαγωνισμό Καγκουρό το 2012, για μαθητές Β, Γ Λυκείου . Δεν είναι ακριβώς η ίδια άσκηση
αλλά λύνεται με τον ίδιο τρόπο. Παραθέτω την εκδοχή του τότε Διαγωνισμού και την λύση που είχα γράψει στο αντίστοιχο βιβλίο μου.
Ένα κομμάτι χαρτί ορθογωνίου σχήματοςδιαστάσεων
διπλώνεται κατά μήκος της ευθείας
έτσι ώστε η κορυφήνα συμπέσει με την
, όπως στην εικόνα. Πόσο είναι το εμβαδόν του τετραπλεύρου
;
 είναι το
είναι το  και επειδή η
και επειδή η  είναι μεσοκάθετη
είναι μεσοκάθετη  , ισούται με το μισό εμβαδόν του ορθογωνίου , είναι δηλαδή
, ισούται με το μισό εμβαδόν του ορθογωνίου , είναι δηλαδή  .
. έχει τετμημένη τριπλάσια της τεταγμένης , δείξτε ότι το συμμετρικό
έχει τετμημένη τριπλάσια της τεταγμένης , δείξτε ότι το συμμετρικό 
 ως προς την μεσοκάθετο της διαγωνίου
ως προς την μεσοκάθετο της διαγωνίου  , έχει τεταγμένη τριπλάσια της τετμημένης !
, έχει τεταγμένη τριπλάσια της τετμημένης !Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες