 της έλλειψης του σχήματος , φέρουμε εφαπτομένη . Υπολογίστε την ελάχιστη τιμή της
της έλλειψης του σχήματος , φέρουμε εφαπτομένη . Υπολογίστε την ελάχιστη τιμή της  .
.Συντονιστής: Τηλέγραφος Κώστας
 της έλλειψης του σχήματος , φέρουμε εφαπτομένη . Υπολογίστε την ελάχιστη τιμή της
της έλλειψης του σχήματος , φέρουμε εφαπτομένη . Υπολογίστε την ελάχιστη τιμή της  .
.Η εφαπτομένη στο σημείο
 της έλλειψης
της έλλειψης 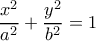 είναι η
είναι η 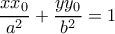 , η οποία έχει κλίση
, η οποία έχει κλίση 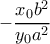 .
. 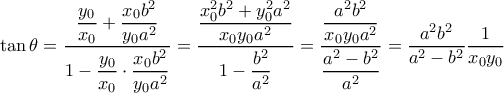
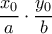 το οποίο είναι βέβαια
το οποίο είναι βέβαια 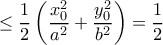 , και λοιπά.
, και λοιπά. της
της  ,
, είναι το σημείο τομής της έλλειψης με την εκ του κέντρου
είναι το σημείο τομής της έλλειψης με την εκ του κέντρου  . (2^ο τεταρτημόριο)
. (2^ο τεταρτημόριο)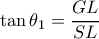 και
και 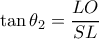 , και για κάθε σημείο της έλλειψης ισχύει
, και για κάθε σημείο της έλλειψης ισχύει 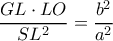
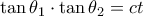 . Τότε λοιπόν
. Τότε λοιπόν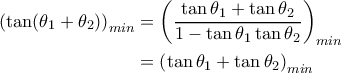
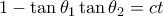 . Και πάλι επειδή
. Και πάλι επειδή 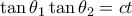 συμπεραίνουμε ότι
συμπεραίνουμε ότι 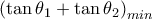 συμβαίνει όταν
συμβαίνει όταν 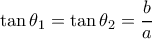
 έχει την μορφή
έχει την μορφή 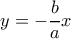 , και επιλύοντας το σύστημα με την έλλειψη βρίσκω
, και επιλύοντας το σύστημα με την έλλειψη βρίσκω 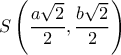 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες