 συνάρτηση συνεχής με την ιδιότητα
συνάρτηση συνεχής με την ιδιότητα 
Αποδείξτε ότι :
1) Αν
 η
η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 
2) Αν
 και
και 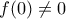 , η
, η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο 
Συντονιστής: chris_gatos
 συνάρτηση συνεχής με την ιδιότητα
συνάρτηση συνεχής με την ιδιότητα 
 η
η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 
 και
και 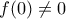 , η
, η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο 
 είναι 1-1 και συνεπώς γν μονότονη λόγω συνέχειας
είναι 1-1 και συνεπώς γν μονότονη λόγω συνέχειας όπου x το f(x) στην αρχική δίνει
όπου x το f(x) στην αρχική δίνει άρα
άρα  και από την αρχική
και από την αρχική  οποτε αν η
οποτε αν η  ήταν αυξουσα πχ για
ήταν αυξουσα πχ για  αντίφαση
αντίφαση διατηρέι πρόσημο πχ
διατηρέι πρόσημο πχ  αν ήταν φθίνουσα τότε
αν ήταν φθίνουσα τότε  αλλά για χ = f(x) η προηγούμενη δίνει
αλλά για χ = f(x) η προηγούμενη δίνει  αντίφαση αρα f γν αύξουσα
αντίφαση αρα f γν αύξουσα εύκολα αποδεικνύεται 1-1 (με την υπόδειξη του Ροδόλφου).
εύκολα αποδεικνύεται 1-1 (με την υπόδειξη του Ροδόλφου). , λόγω και της συνέχειας είναι γνησίως μονότονη
, λόγω και της συνέχειας είναι γνησίως μονότονη είναι γνησίως φθίνουσα, τότε υπάρχει
είναι γνησίως φθίνουσα, τότε υπάρχει  ώστε
ώστε 
 το
το  έχουμε
έχουμε  , άτοπο.
, άτοπο. έχουμε
έχουμε 

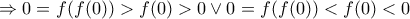 , άτοπο
, άτοποΜέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες