 με πραγματικούς συντελεστές και για το οποίο ισχύει
με πραγματικούς συντελεστές και για το οποίο ισχύει  για κάθε
για κάθε 
όπου
 μια πραγματική σταθερά.
μια πραγματική σταθερά.Να αποδείξετε, ότι
 για κάθε
για κάθε 
Συντονιστής: chris_gatos
 με πραγματικούς συντελεστές και για το οποίο ισχύει
με πραγματικούς συντελεστές και για το οποίο ισχύει  για κάθε
για κάθε 
 μια πραγματική σταθερά.
μια πραγματική σταθερά. για κάθε
για κάθε 
 τότε δεν έχουμε τίποτα να δείξουμε.
τότε δεν έχουμε τίποτα να δείξουμε. τότε η ισότητα γράφεται
τότε η ισότητα γράφεται  οπότε η συνάρτηση
οπότε η συνάρτηση 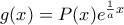 είναι αύξουσα.
είναι αύξουσα.
 για κάθε
για κάθε  οπότε
οπότε  για κάθε
για κάθε 
 τότε η ισότητα γράφεται
τότε η ισότητα γράφεται  οπότε η συνάρτηση
οπότε η συνάρτηση 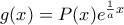 είναι φθίνουσα
είναι φθίνουσα
 για κάθε
για κάθε  οπότε
οπότε  για κάθε
για κάθε  .
.Αλλιώς: Από την δοθείσα συμπεραίνουμε ότι τοmatha έγραψε:Έστω το πολυώνυμομε πραγματικούς συντελεστές και για το οποίο ισχύει
για κάθε
όπουμια πραγματική σταθερά.
Να αποδείξετε, ότι
για κάθε
 είναι άρτιου βαθμού (ή το μηδενικό πολυώνυμο). Άρα έχει ολικό ελάχιστο, έστω στο
είναι άρτιου βαθμού (ή το μηδενικό πολυώνυμο). Άρα έχει ολικό ελάχιστο, έστω στο  , και βέβαια
, και βέβαια  . Άρα για κάθε
. Άρα για κάθε  έχουμε
έχουμε
 και αναλόγως εργαζόμαστε για την περίπτωση
και αναλόγως εργαζόμαστε για την περίπτωση 
 άρα παίρνοντας όρια στο
άρα παίρνοντας όρια στο  βλέπουμε ότι ο μεγιστοβάθμιος όρος του
βλέπουμε ότι ο μεγιστοβάθμιος όρος του  οφείλει να είναι θετικός διαφορετικά ερχόμαστε σε αντίθεση με την
οφείλει να είναι θετικός διαφορετικά ερχόμαστε σε αντίθεση με την  .
. .
.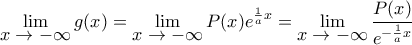 ενός πολυωνύμου
ενός πολυωνύμου  βαθμού
βαθμού  με μεγιστοβάθμιο συντελεστή τον
με μεγιστοβάθμιο συντελεστή τον  εφαρμόζουμε τον κανόνα L' Hospital
εφαρμόζουμε τον κανόνα L' Hospital  φορές για να πάρουμε τελικά
φορές για να πάρουμε τελικά 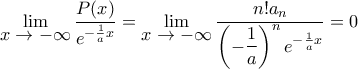
 να είναι
να είναι  και το όριο του εκθετικού
και το όριο του εκθετικού  να είναι
να είναι  , στο τέλος το εκθετικό "τρώει" το πολυώνυμο και το όριο πάει στο
, στο τέλος το εκθετικό "τρώει" το πολυώνυμο και το όριο πάει στο  κάτι το οποίο θεώρησα δεδομένο στην αρχή.
κάτι το οποίο θεώρησα δεδομένο στην αρχή. ''.
''.Σωστά, αλλά νομίζω ότι αυτό που θέλει να πει ο Αλέξανδρος είναι ότι "στην χειρότερη περίπτωση το σύνολο τιμών είναιchris_gatos έγραψε:Καλησπέρα!
Κοιτάζοντας τη λύση του Αλέξανδρου δε με καλύπτει το κλειστό κάτω άκρο του συνόλου τιμών του πολυωνύμου.
Έχω την εντύπωση πως δε δικαιολογείται από κάποια πρόταση.
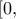 κάτι)". Θα μπορούσε να έγραφε, ορθότερα, "
κάτι)". Θα μπορούσε να έγραφε, ορθότερα, "  κάτι)". Πάντως το επόμενο βήμα στην απόδειξή του είναι σωστό, και η απόδειξη σώζεται.
κάτι)". Πάντως το επόμενο βήμα στην απόδειξή του είναι σωστό, και η απόδειξη σώζεται. είναι σταθερό και συγκεκριμένα το μηδενικό.
είναι σταθερό και συγκεκριμένα το μηδενικό. από το να τα βάλω όλα στο ίδιο τσουβάλι. Να γράψω δηλαδή ότι στην περίπτωση μη μηδενικού πολυωνύμου
από το να τα βάλω όλα στο ίδιο τσουβάλι. Να γράψω δηλαδή ότι στην περίπτωση μη μηδενικού πολυωνύμου  το σύνολο τιμών της
το σύνολο τιμών της  είναι το
είναι το  και στην περίπτωση μηδενικού
και στην περίπτωση μηδενικού  το σύνολο τιμών της
το σύνολο τιμών της  είναι το μονοσύνολο
είναι το μονοσύνολο  . Σε οποιαδήποτε λοιπόν περίπτωση ισχύει
. Σε οποιαδήποτε λοιπόν περίπτωση ισχύει  .
.Δεν αντιλέγω κι εγώ την ίδια λύση έκανα αλλά δεν άγγιζα με τίποτα το μηδέν παρά μόνο με αυτήν την πρόταση που ανέφερα.Mihalis_Lambrou έγραψε:chris_gatos έγραψε:Πάντως το επόμενο βήμα στην απόδειξή του είναι σωστό, και η απόδειξη σώζεται.
Μ.
Να σημειώσω ότι αν
 τότε το συμπέρασμα είναι ότι
τότε το συμπέρασμα είναι ότι  για
για 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες