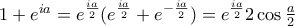Σελίδα 1 από 1
Τι αριθμός είναι το Ρ(-1);;
Δημοσιεύτηκε: Παρ Αύγ 25, 2017 12:14 pm
από chris_gatos
Αν οι ρίζες του πολυωνύμου(με μιγαδικούς συντελεστές)

με

, έχουν ίσα μέτρα, τότε το

είναι
Α) Καθαρός μιγαδικός αριθμός
Β) Καθαρός φανταστικός αριθμός.
Γ) Πραγματικός αριθμός.
Δ) Από άλλον πλανήτη;
Να τεκμηριώσετε την απάντησή σας παρουσιάζοντας μια πλήρη λύση.
Re: Τι αριθμός είναι το Ρ(-1);;
Δημοσιεύτηκε: Σάβ Αύγ 26, 2017 3:25 am
από cretanman
Αν

οι ρίζες, από τύπους Vieta παίρνουμε

κι έτσι παίρνοντας μέτρα και χρησιμοποιώντας την ισότητα των μέτρων των ριζών, όλες ανήκουν στο μοναδιαίο κύκλο. Άρα

για κάθε

με

.
Διακρίνουμε τις εξής περιπτώσεις:

Αν ο

είναι περιττός τότε από τους τύπους Vieta έχουμε:

Επίσης:

Όμοια βγάζουμε ότι:
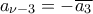


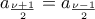
Τελικά λοιπόν χρησιμοποιώντας τις παραπάνω σχέσεις:

άρα

συνεπώς το Γ) είναι η σωστή απάντηση σε αυτή την περίπτωση.

Αν ο

είναι άρτιος τότε με όμοια διαδικασία με την παραπάνω βγάζουμε επίσης ότι

.
Edit (26/8/2017, 11:57): Έκανα διόρθωση
Αλέξανδρος
Re: Τι αριθμός είναι το Ρ(-1);;
Δημοσιεύτηκε: Σάβ Αύγ 26, 2017 11:03 am
από ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ

Εστω

οι ρίζες του πολυωνύμου.
όπου

Επειδή το γινόμενο των ριζών είναι

προκύπτει ότι

Ειναι
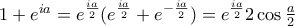
Εχουμε

γιατί

Αρα

Με τον ίδιο τρόπο βρίσκουμε ότι

 με
με  , έχουν ίσα μέτρα, τότε το
, έχουν ίσα μέτρα, τότε το  είναι
είναι  με
με  , έχουν ίσα μέτρα, τότε το
, έχουν ίσα μέτρα, τότε το  είναι
είναι  οι ρίζες, από τύπους Vieta παίρνουμε
οι ρίζες, από τύπους Vieta παίρνουμε  κι έτσι παίρνοντας μέτρα και χρησιμοποιώντας την ισότητα των μέτρων των ριζών, όλες ανήκουν στο μοναδιαίο κύκλο. Άρα
κι έτσι παίρνοντας μέτρα και χρησιμοποιώντας την ισότητα των μέτρων των ριζών, όλες ανήκουν στο μοναδιαίο κύκλο. Άρα  για κάθε
για κάθε  με
με  .
. Αν ο
Αν ο  είναι περιττός τότε από τους τύπους Vieta έχουμε:
είναι περιττός τότε από τους τύπους Vieta έχουμε:

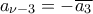


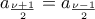

 συνεπώς το Γ) είναι η σωστή απάντηση σε αυτή την περίπτωση.
συνεπώς το Γ) είναι η σωστή απάντηση σε αυτή την περίπτωση.


 προκύπτει ότι
προκύπτει ότι