 θετικοί πραγματικοί αριθμοί τέτοιοι, ώστε το πολυώνυμο
θετικοί πραγματικοί αριθμοί τέτοιοι, ώστε το πολυώνυμο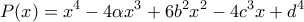
να έχει τέσσερις διαφορετικές θετικές ρίζες.
Τότε να αποδείξετε ότι:

Συντονιστής: chris_gatos
 θετικοί πραγματικοί αριθμοί τέτοιοι, ώστε το πολυώνυμο
θετικοί πραγματικοί αριθμοί τέτοιοι, ώστε το πολυώνυμο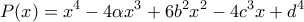

Καταρχάς παρατηρούμε ότι όλες οι ρίζες θα είναι θετικές. Το μηδέν φανερά δεν είναι ρίζα και αρνητική δεν μπορεί να έχειchris_gatos έγραψε: ↑Τρί Σεπ 11, 2018 11:52 pmΈστωθετικοί πραγματικοί αριθμοί τέτοιοι, ώστε το πολυώνυμο
να έχει τέσσερις διαφορετικές θετικές ρίζες.
Τότε να αποδείξετε ότι:

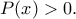 Συνεπώς όλες οι
Συνεπώς όλες οι  θα έχουν και αυτές θετικές
θα έχουν και αυτές θετικές  διακεκριμένες ρίζες. Κάνοντας πράξεις βρίσκουμε
διακεκριμένες ρίζες. Κάνοντας πράξεις βρίσκουμε 
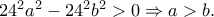 Επίσης,
Επίσης, Αν
Αν  είναι οι τρεις διακεκριμένες θετικές ρίζες του
είναι οι τρεις διακεκριμένες θετικές ρίζες του  τότε από
τότε από  και
και  παίρνουμε
παίρνουμε ![\sum x_ix_j>3\sqrt[3]{(x_1x_2x_3)^2}\Rightarrow 3b^2>3c^2\Rightarrow b>c. \sum x_ix_j>3\sqrt[3]{(x_1x_2x_3)^2}\Rightarrow 3b^2>3c^2\Rightarrow b>c.](/forum/ext/geomar/texintegr/latexrender/pictures/2f411f700c03f14116054ea2daf2596e.png) Τέλος αν
Τέλος αν  είναι οι τέσσερις διακεκριμένες θετικές ρίζες του
είναι οι τέσσερις διακεκριμένες θετικές ρίζες του  τότε πάλι από
τότε πάλι από 
 παίρνουμε
παίρνουμε ![\sum y_iy_jy_l>4\sqrt[4]{(y_1y_2y_3y_4)^3}\Rightarrow 4c^3>4d^3\Rightarrow c>d. \sum y_iy_jy_l>4\sqrt[4]{(y_1y_2y_3y_4)^3}\Rightarrow 4c^3>4d^3\Rightarrow c>d.](/forum/ext/geomar/texintegr/latexrender/pictures/e3358c714433f14fedce6cf98033e2a9.png)
Ανchris_gatos έγραψε: ↑Τρί Σεπ 11, 2018 11:52 pmΈστωθετικοί πραγματικοί αριθμοί τέτοιοι, ώστε το πολυώνυμο
να έχει τέσσερις διαφορετικές θετικές ρίζες.
Τότε να αποδείξετε ότι:

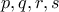 οι θετικές ρίζες έχουμε από Vieta
οι θετικές ρίζες έχουμε από Vieta 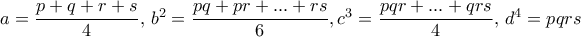 .
. άνισα)
άνισα) ![\dfrac {pqr+...+qrs}{4} > \sqrt [4]{p^3q^3r^3s^3} \dfrac {pqr+...+qrs}{4} > \sqrt [4]{p^3q^3r^3s^3}](/forum/ext/geomar/texintegr/latexrender/pictures/b4454c6c315335dcd10f6659434749a6.png) ή αλλιώς
ή αλλιώς ![c^3> \sqrt [4]{(d^4)^3} c^3> \sqrt [4]{(d^4)^3}](/forum/ext/geomar/texintegr/latexrender/pictures/78cbed99fe8993f2659f35208c53880b.png) , που δίνει
, που δίνει  .
.  και
και 
 (ή αλλιώς symmetric mean inequality)
(ή αλλιώς symmetric mean inequality)![\begin{aligned}\dfrac{a_1+a_2+a_3+a_4}{4} &\geq \sqrt{\dfrac{a_1a_2+a_1a_3+a_1a_4+a_2a_3+a_2a_4+a_3a_4}{6}} \\ &\geq \sqrt[3]{\dfrac{a_1a_2a_3+a_1a_2a_4+a_1a_3a_4+a_2a_3a_4}{4}} \\ &\geq \sqrt[4]{a_1a_2a_3a_4}\end{aligned} \begin{aligned}\dfrac{a_1+a_2+a_3+a_4}{4} &\geq \sqrt{\dfrac{a_1a_2+a_1a_3+a_1a_4+a_2a_3+a_2a_4+a_3a_4}{6}} \\ &\geq \sqrt[3]{\dfrac{a_1a_2a_3+a_1a_2a_4+a_1a_3a_4+a_2a_3a_4}{4}} \\ &\geq \sqrt[4]{a_1a_2a_3a_4}\end{aligned}](/forum/ext/geomar/texintegr/latexrender/pictures/058300ed8bddd224b6e58f1413db9cdb.png)
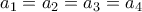 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες