 . Να προσδιορίσετε την ελάχιστη τιμή της παράστασης
. Να προσδιορίσετε την ελάχιστη τιμή της παράστασης  όπου
όπου  σημείο στο επίπεδο του
σημείο στο επίπεδο του  .
.Συντονιστής: chris_gatos
 . Να προσδιορίσετε την ελάχιστη τιμή της παράστασης
. Να προσδιορίσετε την ελάχιστη τιμή της παράστασης  όπου
όπου  σημείο στο επίπεδο του
σημείο στο επίπεδο του  .
.Θα πάρουμε όσο το δυνατόν μικρότερο αριθμητή και μεγαλύτερο παρονομαστή.chris_gatos έγραψε: ↑Παρ Δεκ 28, 2018 1:12 amΈστω τετράγωνο. Να προσδιορίσετε την ελάχιστη τιμή της παράστασης
όπου
σημείο στο επίπεδο του
.
 αντί για
αντί για  και
και  αντί για
αντί για 
 Άρα ο μικρότερος αριθμητής επιτυγχάνεται για
Άρα ο μικρότερος αριθμητής επιτυγχάνεται για  σημείο της
σημείο της  .
.  ή
ή 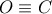 . Πράγματι, αν
. Πράγματι, αν  είναι σημείο της
είναι σημείο της  τότε ο παρονομαστής ελαχιστοποιείται
τότε ο παρονομαστής ελαχιστοποιείται  πρέπει να είναι εκτός της
πρέπει να είναι εκτός της  . Φέρουμε τώρα την
. Φέρουμε τώρα την  και παίρνουμε εκτός
και παίρνουμε εκτός  εσωτερικό του τετραγώνου. Η μεγιστοποίηση είναι άμεση συνέπεια του παρακάτω (ii) (δες εικόνα σχολικό βιβλίο Γεωμετρία Α' Λυκείου).
εσωτερικό του τετραγώνου. Η μεγιστοποίηση είναι άμεση συνέπεια του παρακάτω (ii) (δες εικόνα σχολικό βιβλίο Γεωμετρία Α' Λυκείου). σημείο της
σημείο της 
 και ο μέγιστος παρονομαστής όταν
και ο μέγιστος παρονομαστής όταν  ή
ή 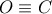 .
.  ικανοποιούνται ταυτόχρονα όταν ικανοποιείται η
ικανοποιούνται ταυτόχρονα όταν ικανοποιείται η  . Τελικά η ελάχιστη τιμή, υποθέτωντας ότι το τετράγωνο έχει πλευρά
. Τελικά η ελάχιστη τιμή, υποθέτωντας ότι το τετράγωνο έχει πλευρά  ,
, 
 είναι το κέντρο του τετραγώνου τότε έχουμε:
είναι το κέντρο του τετραγώνου τότε έχουμε:
 ταυτίζεται με το
ταυτίζεται με το  ή το
ή το  (όπως φαίνεται και στην πρώτη ανισότητα παραπάνω).
(όπως φαίνεται και στην πρώτη ανισότητα παραπάνω).Το αποτέλεσμα πάλι θα ίσχυε σε οποιοδήποτε κυρτό τετράπλευρο μόνο που για τον παρονομαστή θα έπρεπε να ελέγξουμε μία εκ των δύο κορυφών για να δούμε που πετυχαίνουμε μέγιστο. Είναι φανερό από την απόδειξη που έδωσα.S.E.Louridas έγραψε: ↑Κυρ Δεκ 30, 2018 4:44 pmΚαι τώρα ένα βασικό ερώτημα:
Αν αντί για τετράγωνο δινόταν ορθογώνιο το πρόβλημα θα ίσχυε;
Το γνωρίζω αφού το θέμα ήταν δικής μου εισήγησης, ως μέλους και θεματοδότη της επιτροπής διαγωνισμών της Ε.Μ.Ε., και μάλιστα με ορθογώνιο. Όμως αποφασίστηκε να μπεί σε τετράγωνο. Η λύση που προτάθηκε ήταν με μετρική γεωμετρία με ταυτόχρονη εξέταση της γνώσης τηςΛάμπρος Κατσάπας έγραψε: ↑Κυρ Δεκ 30, 2018 4:52 pm... Σημείωση: Όπως ενημερώθηκα το πρόβλημα είναι Ευκλείδης 1997.
 για τυχόντες πραγματικούς
για τυχόντες πραγματικούς  πάνω στην οποία και στηρίχτηκε η λύση. Ταυτόχρονα για ενδεχομένως παρουσιαζόμενη μή μετρική λύση, πιθανό βαθμολογικό ζητούμενο ήταν να διακριθούν οι περιπτώσεις,
πάνω στην οποία και στηρίχτηκε η λύση. Ταυτόχρονα για ενδεχομένως παρουσιαζόμενη μή μετρική λύση, πιθανό βαθμολογικό ζητούμενο ήταν να διακριθούν οι περιπτώσεις,  να είναι εντός του τετραγώνου, ή επί της περιμέτρου και β) άν ήταν εκτός, να αποδεικνυόταν τότε ότι ο αντίστοιχος λόγος δεν υπερέβαινε τον ήδη υπολογισθέντα από την περίπτωση α) minimum.
να είναι εντός του τετραγώνου, ή επί της περιμέτρου και β) άν ήταν εκτός, να αποδεικνυόταν τότε ότι ο αντίστοιχος λόγος δεν υπερέβαινε τον ήδη υπολογισθέντα από την περίπτωση α) minimum. Ακριβώς ήταν η εκδοχή για τετράγωνο από τον Δημήτρη Κοντογιάννη στην πρόταση μου για ορθογώνιο. Προφανώς και σεβάστηκα την πρόταση του Δημήτρη Κοντογιάννη (πραγματικός θρύλος τότε γαρ στους διαγωνισμούς ο Κοντογιάννης και αρκετά μεγαλύτερος ηλικιακά) αν και είχα την άποψη ότι με το τετράγωνο πιθανόν κάποιος εξεταζόμενος να εγκλωβιζόταν σε ειδικώτερες ιδιότητες του τετραγώνου.chris_gatos έγραψε: ↑Τετ Ιαν 02, 2019 3:14 pmΓια να είμαι ειλικρινής είχα δύο πηγές για το θέμα.
Η μια ήταν από ένα παλιό βιβλίο Αναλυτικής Γεωμετρίας του Δ.Κοντογιάννη "Διανυσματικός Λογισμός-Αναλυτική Γεωμετρία", τ.ΙΙ.
Στη σελίδα 104 γράφει (Προτάθηκε από τον συγγραφέα στο διαγωνισμό Ευκλείδη 1997)
 του χώρου και για τυχόν ορθογώνιο
του χώρου και για τυχόν ορθογώνιο  ισχύει ότι
ισχύει ότι  . Αυτό μας πηγαίνει στο θέμα που είδαμε εδώ και που ισχύει στον χώρο με βάση τη πασίγνωστη ανισότητα που ήδη ανέφερα πιό πάνω και απλά προσαρμόστηκε καταρχάς στο ότι το
. Αυτό μας πηγαίνει στο θέμα που είδαμε εδώ και που ισχύει στον χώρο με βάση τη πασίγνωστη ανισότητα που ήδη ανέφερα πιό πάνω και απλά προσαρμόστηκε καταρχάς στο ότι το  ανήκει στο επίπεδο του
ανήκει στο επίπεδο του  επειδή θέλαμε να μην εμπλακούν οι λύτες εκεί, δηλαδή στον χώρο
επειδή θέλαμε να μην εμπλακούν οι λύτες εκεί, δηλαδή στον χώρο  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες