 ισχύει:
ισχύει:
Να βρείτε την ελάχιστη τιμή που μπορεί να λάβει το
 .
.Συντονιστής: chris_gatos
 ισχύει:
ισχύει:
 .
.
 θετικό και «προς στιγμήν σταθερό», η ελάχιστη τιμή του
θετικό και «προς στιγμήν σταθερό», η ελάχιστη τιμή του  προκύπτει όταν
προκύπτει όταν  , οπότε είναι
, οπότε είναι  ,
, , οπότε η δεύτερη ισότητα γίνεται
, οπότε η δεύτερη ισότητα γίνεται  ,
,  είναι
είναι  .
. τότε
τότε  , οπότε δεν έχουμε ελάχιστο.
, οπότε δεν έχουμε ελάχιστο. θετικό και σταθερό, οπότε
θετικό και σταθερό, οπότε  κ.ο.κ.
κ.ο.κ. και προσθέτω
και προσθέτω 

 θα είναι
θα είναι  με το ίσον όταν
με το ίσον όταν  , οπότε
, οπότε 
 , τότε
, τότε  , με το ελάχιστο όταν
, με το ελάχιστο όταν  .
. , τότε
, τότε 
 , που επαληθεύει την αρχική, αφού το σύστημα
, που επαληθεύει την αρχική, αφού το σύστημα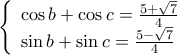 είναι συμβιβαστό (δίνει πράγματι
είναι συμβιβαστό (δίνει πράγματι  ).
). μεταβαίνουμε στο ελάχιστο του
μεταβαίνουμε στο ελάχιστο του  . Αφήνω, βεβαίως, την ανάρτησή μου με τα κενά της ώστε να συμπληρωθεί, αν γίνεται, ή αλλιώς να αποτελέσει αφορμή για συζήτηση.
. Αφήνω, βεβαίως, την ανάρτησή μου με τα κενά της ώστε να συμπληρωθεί, αν γίνεται, ή αλλιώς να αποτελέσει αφορμή για συζήτηση. κάτω από τις συνθήκες
κάτω από τις συνθήκες  και
και 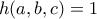 , όπου
, όπου  και
και  .
.  δεν είναι κυκλικά συμμετρική ως προς
δεν είναι κυκλικά συμμετρική ως προς  ,
,  και
και  .
.  και προσθέτω
και προσθέτω 

 θα είναι
θα είναι 














 θα πρέπει να βόσκει στον κύκλο
θα πρέπει να βόσκει στον κύκλο 
 .
.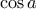 γίνεται ελάχιστο όταν το
γίνεται ελάχιστο όταν το είναι το σημείο
είναι το σημείο



 είναι το σημείο τομής με τη μεγαλύτερη τετμημένη.
είναι το σημείο τομής με τη μεγαλύτερη τετμημένη.Ευχαριστώ Γιώργο.Αλλά όπως θα δεις και παραπάνω μπέρδεψα την τετμημένη με την τεταγμένη.Γιώργος Ρίζος έγραψε: ↑Τρί Απρ 16, 2019 8:35 pmΑναρτώ το σχήμα για την τελευταία γεωμετρική λύση του Σταύρου.
Το σημείοείναι το σημείο τομής με τη μεγαλύτερη τετμημένη.
16-04-2019 Γεωμετρία.png


 (1)
(1)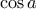 αρκεί να βρούμε το μέγιστο του
αρκεί να βρούμε το μέγιστο του  .
.

 δίνει η δεύτερη που γράφεται
δίνει η δεύτερη που γράφεται 


 είναι μέγιστο.
είναι μέγιστο.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες