 τέτοιοι ώστε να ισχύει:
τέτοιοι ώστε να ισχύει:  .
.Να αποδείξετε ότι:
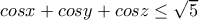 .
.Συντονιστής: chris_gatos
 τέτοιοι ώστε να ισχύει:
τέτοιοι ώστε να ισχύει:  .
.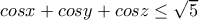 .
. και
και 

 απ' όπου
απ' όπου  κι έτσι έχουμε το ζητούμενο (και κατιτίς παραπάνω).
κι έτσι έχουμε το ζητούμενο (και κατιτίς παραπάνω). Θετω






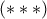


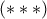
 .
.

 , άτοπο.
, άτοπο.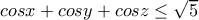 .
.Έστω
 όπου
όπου ![a,b,c \in [-1,1] a,b,c \in [-1,1]](/forum/ext/geomar/texintegr/latexrender/pictures/338ebff4fbfaaca839cc4ed7a5c42ff8.png) . Από την κοιλότητα της
. Από την κοιλότητα της  (υπόψη δεν χρειάζεται να παραγωγίσουμε: Είναι ημικύκλιο) έχουμε
(υπόψη δεν χρειάζεται να παραγωγίσουμε: Είναι ημικύκλιο) έχουμε  , και λοιπά.
, και λοιπά. και
και 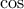 . Έχουμε λοιπόν.
. Έχουμε λοιπόν. οπότε
οπότε  , όπως θέλαμε.
, όπως θέλαμε.  . Επίσης, δεδομένης μιας τέτοιας
. Επίσης, δεδομένης μιας τέτοιας  (όμοια για τις υπόλοιπες) θεωρούμε γωνία
(όμοια για τις υπόλοιπες) θεωρούμε γωνία  του πρώτου τεταρτημορίου για την οποία ισχύει
του πρώτου τεταρτημορίου για την οποία ισχύει  . Για παράδειγμα αν η
. Για παράδειγμα αν η  είναι στο β' τεταρτημόριο παίρνουμε
είναι στο β' τεταρτημόριο παίρνουμε  , αν είναι στο τρίτο παίρνουμε
, αν είναι στο τρίτο παίρνουμε  και στο τέταρτο παίρνουμε
και στο τέταρτο παίρνουμε  . Σε όλες τις περιπτώσεις έχουμε
. Σε όλες τις περιπτώσεις έχουμε  αλλά και επίσης
αλλά και επίσης  . Ειδικά έχουμε
. Ειδικά έχουμε  αφού το εκάστοτε δεξί μέλος είναι
αφού το εκάστοτε δεξί μέλος είναι  ενώ το αριστερό είναι ίσο του ή αντίθετο. Άρα
ενώ το αριστερό είναι ίσο του ή αντίθετο. Άρα  οπότε με χρήση αυτού που μόλις αποδείξαμε, έχουμε
οπότε με χρήση αυτού που μόλις αποδείξαμε, έχουμε  , όπως θέλαμε.
, όπως θέλαμε.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες