![4\left [ \left ( 1-x \right )^2+\left ( x-y \right )^2+\left ( y-w \right )^2+w^2 \right ]=1 4\left [ \left ( 1-x \right )^2+\left ( x-y \right )^2+\left ( y-w \right )^2+w^2 \right ]=1](/forum/ext/geomar/texintegr/latexrender/pictures/b986fad4df152d18e6b38f2856cfdaab.png)
Μία εξίσωση, τρείς αγνωστοι.
Συντονιστής: chris_gatos
- chris_gatos
- Επιμελητής
- Δημοσιεύσεις: 6962
- Εγγραφή: Κυρ Δεκ 21, 2008 9:03 pm
- Τοποθεσία: Ανθούπολη
Μία εξίσωση, τρείς αγνωστοι.
Να λύσετε στο σύνολο των πραγματικών την εξίσωση:
![4\left [ \left ( 1-x \right )^2+\left ( x-y \right )^2+\left ( y-w \right )^2+w^2 \right ]=1 4\left [ \left ( 1-x \right )^2+\left ( x-y \right )^2+\left ( y-w \right )^2+w^2 \right ]=1](/forum/ext/geomar/texintegr/latexrender/pictures/b986fad4df152d18e6b38f2856cfdaab.png)
![4\left [ \left ( 1-x \right )^2+\left ( x-y \right )^2+\left ( y-w \right )^2+w^2 \right ]=1 4\left [ \left ( 1-x \right )^2+\left ( x-y \right )^2+\left ( y-w \right )^2+w^2 \right ]=1](/forum/ext/geomar/texintegr/latexrender/pictures/b986fad4df152d18e6b38f2856cfdaab.png)
Χρήστος Κυριαζής
Λέξεις Κλειδιά:
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15764
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Μία εξίσωση, τρείς αγνωστοι.


οπότε έχουμε ισότητα παντού, και ειδικά στην
 . Έπεται (άμεσο) ότι
. Έπεται (άμεσο) ότι  και άρα
και άρα 
- S.E.Louridas
- Δημοσιεύσεις: 5956
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: Μία εξίσωση, τρείς αγνωστοι.


οπότε έχουμε

S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
- nsmavrogiannis
- Επιμελητής
- Δημοσιεύσεις: 4455
- Εγγραφή: Σάβ Δεκ 20, 2008 7:13 pm
- Τοποθεσία: Αθήνα
- Επικοινωνία:
Re: Μία εξίσωση, τρείς αγνωστοι.
Μία με ύλη Α΄Λυκείου μεν με περισσότερη δουλειά δε:
Η εξίσωση γράφεται:
![8w^{2}-8yw+\left[ 4\left( 1-x\right) ^{2}+4\left( x-y\right) ^{2}+4y^{2}-1\right] =0 8w^{2}-8yw+\left[ 4\left( 1-x\right) ^{2}+4\left( x-y\right) ^{2}+4y^{2}-1\right] =0](/forum/ext/geomar/texintegr/latexrender/pictures/09734b0a04cc50b6fcae9f9970778f8b.png)
και θεωρούμενη ως εξίσωση με άγνωστο έχει διακρίνουσα:
έχει διακρίνουσα:

η οποία πρέπει να είναι μη αρνητική.
Το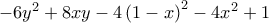 θεωρούμενο ως τριώνυμο του
θεωρούμενο ως τριώνυμο του  έχει διακρίνουσα
έχει διακρίνουσα

που επίσης πρέπει να είναι μη αρνητική.
Άρα οπότε
οπότε

και .
.
Για αυτές τις τιμές των ,
,  η αρχική εξίσωση δίνει
η αρχική εξίσωση δίνει 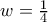 .
.
Την λύση την έγραψα πιο πολύ ως μια ακόμη απόδειξη της σημασίας που έχει η θεωρητική γνώση για να ευκολύνουμε την ζωή μας όπως, στη συγκεκριμένη περίπτωση, έδειξαν οι λύσεις του Μιχάλη και του Σωτήρη.
Η εξίσωση γράφεται:
![8w^{2}-8yw+\left[ 4\left( 1-x\right) ^{2}+4\left( x-y\right) ^{2}+4y^{2}-1\right] =0 8w^{2}-8yw+\left[ 4\left( 1-x\right) ^{2}+4\left( x-y\right) ^{2}+4y^{2}-1\right] =0](/forum/ext/geomar/texintegr/latexrender/pictures/09734b0a04cc50b6fcae9f9970778f8b.png)
και θεωρούμενη ως εξίσωση με άγνωστο
 έχει διακρίνουσα:
έχει διακρίνουσα:
η οποία πρέπει να είναι μη αρνητική.
Το
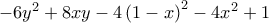 θεωρούμενο ως τριώνυμο του
θεωρούμενο ως τριώνυμο του  έχει διακρίνουσα
έχει διακρίνουσα 
που επίσης πρέπει να είναι μη αρνητική.
Άρα
 οπότε
οπότε 
και
 .
. Για αυτές τις τιμές των
 ,
,  η αρχική εξίσωση δίνει
η αρχική εξίσωση δίνει 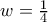 .
. Την λύση την έγραψα πιο πολύ ως μια ακόμη απόδειξη της σημασίας που έχει η θεωρητική γνώση για να ευκολύνουμε την ζωή μας όπως, στη συγκεκριμένη περίπτωση, έδειξαν οι λύσεις του Μιχάλη και του Σωτήρη.
Αν κανείς δεν ελπίζει, δεν θα βρεί το ανέλπιστο, οι δρόμοι για το ανεξερεύνητο θα είναι κλειστοί.
Ηράκλειτος
Ηράκλειτος
-
Παύλος Μαραγκουδάκης
- Επιμελητής
- Δημοσιεύσεις: 1513
- Εγγραφή: Παρ Ιαν 30, 2009 1:45 pm
- Τοποθεσία: Πειραιάς
- Επικοινωνία:
Re: Μία εξίσωση, τρείς αγνωστοι.
Καλησπέρα σας!
Είδα καλή παρέα και μπήκα!
Αισθάνθηκα σαν να περπατούσα στην παλιά μου γειτονιά και να είδα φίλους καλούς που με κάλεσαν στο τραπέζι τους!
Θέτω



Τότε Άρα
Άρα
 οπότε
οπότε




Είδα καλή παρέα και μπήκα!
Αισθάνθηκα σαν να περπατούσα στην παλιά μου γειτονιά και να είδα φίλους καλούς που με κάλεσαν στο τραπέζι τους!
Θέτω




Τότε
 Άρα
Άρα οπότε
οπότε



Στάλα τη στάλα το νερό το μάρμαρο τρυπά το,
εκείνο που μισεί κανείς γυρίζει κι αγαπά το.
εκείνο που μισεί κανείς γυρίζει κι αγαπά το.
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15764
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Μία εξίσωση, τρείς αγνωστοι.
Ξαναγράφω την λύση που έδωσα αλλά τώρα προσαρμοσμένη σε γνώσεις Α' Λυκείου ώστε να είναι χρήσιμη σε περισσότερους.
Θα χησιμοποιήσω μόνο την ανισότητα με ισότητα αν και μόνον αν
με ισότητα αν και μόνον αν  (ισοδυναμεί με την
(ισοδυναμεί με την  ).
).
Για


 , οπότε
, οπότε  , έχουμε
, έχουμε

άρα έχουμε ισότητα παντού. Ειδικά από την πρώτη ανισότητα έχουμε και
και  και από την δεύτερη
και από την δεύτερη  , οπότε τελικά
, οπότε τελικά  , και λοιπά.
, και λοιπά.
Θα χησιμοποιήσω μόνο την ανισότητα
 με ισότητα αν και μόνον αν
με ισότητα αν και μόνον αν  (ισοδυναμεί με την
(ισοδυναμεί με την  ).
).Για



 , οπότε
, οπότε  , έχουμε
, έχουμε
άρα έχουμε ισότητα παντού. Ειδικά από την πρώτη ανισότητα έχουμε
 και
και  και από την δεύτερη
και από την δεύτερη  , οπότε τελικά
, οπότε τελικά  , και λοιπά.
, και λοιπά.- S.E.Louridas
- Δημοσιεύσεις: 5956
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: Μία εξίσωση, τρείς αγνωστοι.
Πάντα στο πνεύμα του Μαθηματικού πλουραλισμού επιλύσων.
Με βάση την ταυτότητα του Lagrange, για ( Σε τέως βιβλίο Άλγεβρας της Α' Λυκείου (Δ' λυκείου Θετικής Κατεύθυνσης) των Θ.Βαβαλέτσκου, Γ. Μπούσγου του ΟΕΔΒ), που ξεκινούσε με το κεφάλαιο Μαθηματική Λογική (υποχρεωτική η διδασκαλία της και η εξέταση της) εύκολα παίρνουμε:
( Σε τέως βιβλίο Άλγεβρας της Α' Λυκείου (Δ' λυκείου Θετικής Κατεύθυνσης) των Θ.Βαβαλέτσκου, Γ. Μπούσγου του ΟΕΔΒ), που ξεκινούσε με το κεφάλαιο Μαθηματική Λογική (υποχρεωτική η διδασκαλία της και η εξέταση της) εύκολα παίρνουμε:


(*) Ταυτότητα Lagrange:


Με βάση την ταυτότητα του Lagrange, για
 ( Σε τέως βιβλίο Άλγεβρας της Α' Λυκείου (Δ' λυκείου Θετικής Κατεύθυνσης) των Θ.Βαβαλέτσκου, Γ. Μπούσγου του ΟΕΔΒ), που ξεκινούσε με το κεφάλαιο Μαθηματική Λογική (υποχρεωτική η διδασκαλία της και η εξέταση της) εύκολα παίρνουμε:
( Σε τέως βιβλίο Άλγεβρας της Α' Λυκείου (Δ' λυκείου Θετικής Κατεύθυνσης) των Θ.Βαβαλέτσκου, Γ. Μπούσγου του ΟΕΔΒ), που ξεκινούσε με το κεφάλαιο Μαθηματική Λογική (υποχρεωτική η διδασκαλία της και η εξέταση της) εύκολα παίρνουμε: 

(*) Ταυτότητα Lagrange:


τελευταία επεξεργασία από S.E.Louridas σε Τρί Δεκ 15, 2020 11:43 am, έχει επεξεργασθεί 2 φορές συνολικά.
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
Re: Μία εξίσωση, τρείς αγνωστοι.
Θεωρώ το ορθογώνιο  , με
, με  . Υπάρχει σημείο εσωτερικό
. Υπάρχει σημείο εσωτερικό  του
του  , τέτοιο
, τέτοιο
ώστε : . Για το σημείο
. Για το σημείο  , ισχύει ότι :
, ισχύει ότι :  ( η δοθείσα ) .
( η δοθείσα ) .
Θα δείξουμε ότι το μέσο του του τμήματος
του τμήματος  , δίνει μία λύση του προβλήματος . Πράγματι :
, δίνει μία λύση του προβλήματος . Πράγματι :
 , ή :
, ή :  , ισοδύναμα :
, ισοδύναμα :
 , (
, (  μέσο του
μέσο του  ) , οπότε :
) , οπότε :  .
.
Φυσικά τα παραπάνω δεν αποτελούν λύση του προβλήματος , παρά μια προσπάθεια γεωμετρικής
ερμηνείας ( μάλλον όχι επιτυχούς ) , αλλά την αφήνω : ίσως κάποιος διαβλέψει κάτι
 , με
, με  . Υπάρχει σημείο εσωτερικό
. Υπάρχει σημείο εσωτερικό  του
του  , τέτοιο
, τέτοιο ώστε :
 . Για το σημείο
. Για το σημείο  , ισχύει ότι :
, ισχύει ότι :  ( η δοθείσα ) .
( η δοθείσα ) .Θα δείξουμε ότι το μέσο του
 του τμήματος
του τμήματος  , δίνει μία λύση του προβλήματος . Πράγματι :
, δίνει μία λύση του προβλήματος . Πράγματι : , ή :
, ή :  , ισοδύναμα :
, ισοδύναμα :  , (
, (  μέσο του
μέσο του  ) , οπότε :
) , οπότε :  .
.Φυσικά τα παραπάνω δεν αποτελούν λύση του προβλήματος , παρά μια προσπάθεια γεωμετρικής
ερμηνείας ( μάλλον όχι επιτυχούς ) , αλλά την αφήνω : ίσως κάποιος διαβλέψει κάτι
Re: Μία εξίσωση, τρείς αγνωστοι.
Καλησπέρα!
Άλλη μια γεωμετρική προσέγγιση:
Θεωρώ τρίγωνο , με
, με  .
.
Έστω το μέσο του
το μέσο του  .
.
Ισχύουν :

και

και άρα
 .
.
Από το 1ο θεώρημα διαμέσων έχω:
 .
.
Άρα,

και .
.
Άρα, .
.
Τελικά
 .
.
Άλλη μια γεωμετρική προσέγγιση:
Θεωρώ τρίγωνο
 , με
, με  .
.Έστω
 το μέσο του
το μέσο του  .
.Ισχύουν :

και

και άρα
 .
.Από το 1ο θεώρημα διαμέσων έχω:
 .
.Άρα,

και
 .
.Άρα,
 .
.Τελικά
 .
.Κώστας
- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5285
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: Μία εξίσωση, τρείς αγνωστοι.
Καλησπέρα σε όλους. Φαντάζομαι δεν θα περιμένει κι άλλη λύση ο Χρήστος, απλώς να κάνω μια ιστορική αναδρομή.
Τα παλιότερα χρόνια, όταν τα προβλήματα min-max λυνόταν με αλγεβρικές μεθόδους, εφαρμοζόταν, μεταξύ των άλλων, και το θεώρημα:
Όταν το άθροισμα θετικών μεταβλητών είναι σταθερό, το άθροισμα των τετραγώνων τους παίρνει την ελάχιστη τιμή τους όταν είναι ίσοι μεταξύ τους, (αν μπορεί αυτό να συμβεί).
Εδώ, λοιπόν, το πρώτο που κοιτάς είναι αν η ισότητα θα συμβεί σε μια ακραία τιμή.
παρατηρούμε ότι είναι ,
,
Άρα έχουμε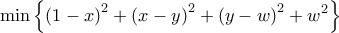 , όταν
, όταν

Παρατηρούμε ότι το minimum είναι ίσο με , άρα οι παραπάνω τιμές των
, άρα οι παραπάνω τιμές των  είναι οι μοναδικές λύσεις της δοθείσης εξίσωσης.
είναι οι μοναδικές λύσεις της δοθείσης εξίσωσης.
Ουσιαστικά είναι εφαρμογή της ανισότητας που χρησιμοποίησε ο Μιχάλης παραπάνω.

(γενικότερα)
Δεν γνωρίζω αν οι συγγραφείς σχολικών και φροντιστηριακών συγγραμμάτων της εποχής χρησιμοποίησαν στην απόδειξη του θεωρήματος τις παραπάνω ανισότητες. Δεν τις συναντάμε συχνά στη βιβλιογραφία της εποχής, (τουλάχιστον στα σχολικά μαθηματικά). Επιπλέον, παρατηρήστε, ότι απαιτούν οι όροι να είναι θετικοί, δίχως αυτό να είναι πάντα απαραίτητο.
Τα παλιότερα χρόνια, όταν τα προβλήματα min-max λυνόταν με αλγεβρικές μεθόδους, εφαρμοζόταν, μεταξύ των άλλων, και το θεώρημα:
Όταν το άθροισμα θετικών μεταβλητών είναι σταθερό, το άθροισμα των τετραγώνων τους παίρνει την ελάχιστη τιμή τους όταν είναι ίσοι μεταξύ τους, (αν μπορεί αυτό να συμβεί).
Εδώ, λοιπόν, το πρώτο που κοιτάς είναι αν η ισότητα θα συμβεί σε μια ακραία τιμή.
παρατηρούμε ότι είναι
 ,
, Άρα έχουμε
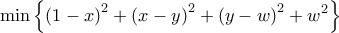 , όταν
, όταν 
Παρατηρούμε ότι το minimum είναι ίσο με
 , άρα οι παραπάνω τιμές των
, άρα οι παραπάνω τιμές των  είναι οι μοναδικές λύσεις της δοθείσης εξίσωσης.
είναι οι μοναδικές λύσεις της δοθείσης εξίσωσης.Ουσιαστικά είναι εφαρμογή της ανισότητας που χρησιμοποίησε ο Μιχάλης παραπάνω.

(γενικότερα)

Δεν γνωρίζω αν οι συγγραφείς σχολικών και φροντιστηριακών συγγραμμάτων της εποχής χρησιμοποίησαν στην απόδειξη του θεωρήματος τις παραπάνω ανισότητες. Δεν τις συναντάμε συχνά στη βιβλιογραφία της εποχής, (τουλάχιστον στα σχολικά μαθηματικά). Επιπλέον, παρατηρήστε, ότι απαιτούν οι όροι να είναι θετικοί, δίχως αυτό να είναι πάντα απαραίτητο.
- chris_gatos
- Επιμελητής
- Δημοσιεύσεις: 6962
- Εγγραφή: Κυρ Δεκ 21, 2008 9:03 pm
- Τοποθεσία: Ανθούπολη
Re: Μία εξίσωση, τρείς αγνωστοι.
Μένω άναυδος από την παροχή λύσεων!
Μαγεία!
Ευχαριστώ όλους όσους ασχολήθηκαν!
Υ.Γ: Η άσκηση αντλήθηκε από ένα παλιό θαυματουργό βιβλιαράκι με τίτλο "Τριώνυμο" και συγγραφέα τον Δημήτρη Μάγκο .
Μαγεία!
Ευχαριστώ όλους όσους ασχολήθηκαν!
Υ.Γ: Η άσκηση αντλήθηκε από ένα παλιό θαυματουργό βιβλιαράκι με τίτλο "Τριώνυμο" και συγγραφέα τον Δημήτρη Μάγκο .
Χρήστος Κυριαζής
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες
