Συνθήκη Lipschitz

#1

Έστω

μια συνάρτηση ορισμένη σε ένα διάστημα $\Delta$ . Θα λέμε ότι η

ικανοποιεί μία συνθήκη Lipschitz στο $\Delta$
αν υπάρχει αριθμός

τέτοιος ώστε:
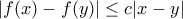$|f(x)-f(y)| \leq c |x-y|$ για όλα τα $x, y \in \Delta$ .
α) Να αποδείξετε ότι κάθε παραγωγίσιμη κυρτή συνάρτηση σε ένα κλειστό διάστημα $\Delta=[\alpha, \beta]$ ικανοποιεί μία συνθήκη Lipschitz στο $\Delta$ .
β) Να εξετάσετε αν ισχύει το αντίστροφο του α).

stranger · #2

Για το α)
Αφού η

είναι κυρτή στο [a,b]

έχουμε ότι $f^{\prime}(a) \leq f^{\prime}(x) \leq f^{\prime}(b)$
Άρα η $f^{\prime}$ είναι φραγμένη,δηλ. υπάρχει C>0

ώστε $|f^{\prime}(x)| \leq C$ για κάθε

.
Από ΘΜΤ παίρνουμε $|\frac{f(x)-f(y)}{x-y}| \leq C$ για κάθε x,y

με $x \neq y$ και το ζητούμενο έπεται.
Για το β) αν πάρουμε $f(x)=\log x$ στο $[\frac{1}{2},1]$ τότε η

δεν είναι κυρτή και είναι Lipschitz, αφού η παραγωγός της είναι φραγμένη στο $[\frac{1}{2},1]$ , άρα δεν ισχύει το αντίστροφο του α).
Σημείωση: Χρησιμοποίησα τον σχολικό ορισμό της κυρτότητας.

Συνθήκη Lipschitz

Συνθήκη Lipschitz

Re: Συνθήκη Lipschitz

Μέλη σε σύνδεση