 .
.Αν η ανισοισότητα
 ισχύει για κάθε
ισχύει για κάθε ![x \in [1,2] x \in [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/5e45ec4bc7e60fb589a8593c3007ea20.png)
τότε να υπολογίσετε την τιμή της παράστασης

Συντονιστής: chris_gatos
 .
. ισχύει για κάθε
ισχύει για κάθε ![x \in [1,2] x \in [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/5e45ec4bc7e60fb589a8593c3007ea20.png)

Δεν υπάρχουνchris_gatos έγραψε: ↑Κυρ Ιαν 21, 2024 11:43 pmΈστω οι πραγματικοί αριθμοί.
Αν η ανισοισότηταισχύει για κάθε
τότε να υπολογίσετε την τιμή της παράστασης

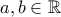 ώστε να ισχύει
ώστε να ισχύει ![\displaystyle{|x^2-a x+b|\leq\frac{1}{8}, \ \ \forall x\in [1,2]} \displaystyle{|x^2-a x+b|\leq\frac{1}{8}, \ \ \forall x\in [1,2]}](/forum/ext/geomar/texintegr/latexrender/pictures/1f0de4d9df4782354c0a2638e7d21516.png)
![\displaystyle{f(x)=x^2-ax+b-\frac{1}{8}\leq0, \ \ \forall x\in [1,2]} \displaystyle{f(x)=x^2-ax+b-\frac{1}{8}\leq0, \ \ \forall x\in [1,2]}](/forum/ext/geomar/texintegr/latexrender/pictures/96044dba677e913cbb3ce9231990916a.png) και
και ![\displaystyle{g(x)=x^2-ax+b+\frac{1}{8}\geq0, \ \ \forall x\in [1,2]} \displaystyle{g(x)=x^2-ax+b+\frac{1}{8}\geq0, \ \ \forall x\in [1,2]}](/forum/ext/geomar/texintegr/latexrender/pictures/d5f4e9dc260dab53131dac1b6b145c72.png)
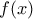 θα πρέπει να έχει δύο ρίζες
θα πρέπει να έχει δύο ρίζες 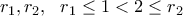 , οι οποίες επαληθεύουν την
, οι οποίες επαληθεύουν την 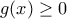 .
. έχει δύο άνισες ρίζες αυτές θα πρέπει να είναι, και οι δύο, μικρότερες ή ίσες από την
έχει δύο άνισες ρίζες αυτές θα πρέπει να είναι, και οι δύο, μικρότερες ή ίσες από την 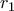 ή μεγαλύτερες ή ίσες από την
ή μεγαλύτερες ή ίσες από την 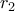
 ρίζα του
ρίζα του  , τότε θα πρέπει
, τότε θα πρέπει 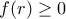 , το οποίο είναι είναι αδύνατο.
, το οποίο είναι είναι αδύνατο. να έχει
να έχει 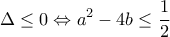 .
.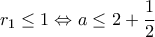 και
και 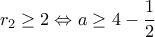 το οποίο είναι αδύνατο.
το οποίο είναι αδύνατο. και
και 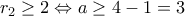 .
. 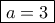 , με την ισότητα να ισχύει όταν
, με την ισότητα να ισχύει όταν 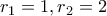 .
. 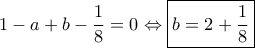 ....
....

 και το ζεύγος είναι μοναδικό.
και το ζεύγος είναι μοναδικό. παίρνουμε ότι
παίρνουμε ότι 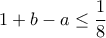 Για
Για  παίρνουμε
παίρνουμε 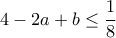 Τέλος, για
Τέλος, για 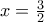 έχουμε
έχουμε 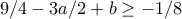
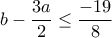 ενώ η δεύτερη δίνει
ενώ η δεύτερη δίνει 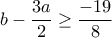
 ,
, 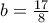 .
. 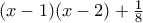 . Στο διάστημα
. Στο διάστημα ![[1,2] [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/f79408e5ca998cd53faf44af31e6eb45.png) παίρνει μέγιστη και ελάχιστη τιμή, τις
παίρνει μέγιστη και ελάχιστη τιμή, τις  (για
(για  και
και  ) και
) και 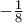 για
για 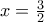 , αντίστοιχα.
, αντίστοιχα.Χρήστο...εντάξει είναι εκτός ανchris_gatos έγραψε: ↑Δευ Ιαν 22, 2024 1:03 pmΕυχαριστώ πολύ για την λύση (πολύ απλούστερη της δικής μου) Σιλουανέ!
Κύριε abgd ευχαριστώ πολύ για την ένστασή σας, θα την μελετήσω.
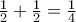


![4\left | x^2-ax+b \right |\leq \dfrac{1}{2}\Rightarrow \left | (2x)^2-2a(2x) +4b \right |\leq \dfrac{1}{2},\forall x\in [1,2] 4\left | x^2-ax+b \right |\leq \dfrac{1}{2}\Rightarrow \left | (2x)^2-2a(2x) +4b \right |\leq \dfrac{1}{2},\forall x\in [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/c8ddc65e7c96b78da81bd3b609cf1b6e.png)
![\left | y^2-2ay+4b \right |\leq \dfrac{1}{2},\forall y\in [2,4] \left | y^2-2ay+4b \right |\leq \dfrac{1}{2},\forall y\in [2,4]](/forum/ext/geomar/texintegr/latexrender/pictures/f051839f5239cfc69decdbfa188182b7.png) .
.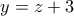 και παίρνω
και παίρνω ![\left | (z+3)^2-2(z+3)a+4b \right |\leq \dfrac{1}{2}\Rightarrow \left | z^2+(6-2a)z+9-6a+4b \right |\leq \dfrac{1}{2}, \forall z\in [-1,1] \left | (z+3)^2-2(z+3)a+4b \right |\leq \dfrac{1}{2}\Rightarrow \left | z^2+(6-2a)z+9-6a+4b \right |\leq \dfrac{1}{2}, \forall z\in [-1,1]](/forum/ext/geomar/texintegr/latexrender/pictures/d67ea8a66adc413b9e78a463ffd494cf.png) .
.![[-1,1] [-1,1]](/forum/ext/geomar/texintegr/latexrender/pictures/d060b17b29e0dae91a1cac23ea62281a.png) είναι
είναι  και πιάνεται για το πολυώνυμο
και πιάνεται για το πολυώνυμο 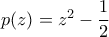 (βάσει της θεωρίας πολυωνύμων Chebychev).
(βάσει της θεωρίας πολυωνύμων Chebychev).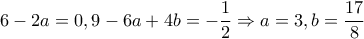 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 11 επισκέπτες