Πραγματικοί Αριθμοί Από τον Ευκλείδη στον Κολμογκόροβ

Al.Koutsouridis · #1

Το παρακάτω μικρό άρθρο είχε πρωτοεμφανιστεί στην περιοδική έκδοση του «Επιτυχίες της μαθηματικής επιστήμης», σειρά 1, έκδοση 1, 1946 και επανεμφανίστηκε στο περιοδικό «Μαθηματική Εκπαίδευση» σειρά 2, τεύχος 2, 1957 από όπου και το μεταφέρω. Δίνει μια διαφορετική κατασκευή των πραγματικών αριθμών. Σε ποιο αναλυτική μορφή είχε χρησιμοποιηθεί για την εισαγωγή των πραγματικών αριθμών σε μερικά Παιδαγωγικά Ινστιτούτα, πιθανόν και σε φυσικό-μαθηματικά σχολεία. (Σημείωση: ο όρος Παιδαγωγικό Ινστιτούτο στο ρωσικό σύστημα εκπαίδευσης δεν συμπίπτει με τον ελληνικό όρο. Εδώ εννοούνται πανεπιστημιακές σχολές 4-ετούς ή, 5-ετούς φοίτησης για τις φυσικομαθηματικές σχολές, που κύριο σκοπό είχαν την στελέχωση του τομέα της εκπαίδευσης, καθηγητές κτλ.)

Πάνω στην θεμελίωση των πραγματικών αριθμών. Α. Ν. Κολμογκόροβ.

Συνήθως για την κατασκευή της θεωρίας των πραγματικών αριθμών προϋποθέτουν την ήδη κατασκευασθήσα θεωρία ρητών αριθμών. Είναι δυνατόν να προσεγγίσουμε διαφορετικά και να εισάγουμε τους πραγματικούς αριθμούς κατευθείαν μετά τους ακέραιους. Ο προτεινόμενος παρακάτω τρόπος θεμελίωσης των πραγματικών αριθμών δεν είναι τίποτα διαφορετικό από ότι ένας σύγχρονος φορμαλισμός της ευκλείδειας θεωρίας μέτρησης. Για λόγους επίτευξης μεγαλύτερης απλότητας και εγγύτητας στην κλασική ευκλείδεια κατασκευή, κατασκευάζεται το σύστημα των θετικών πραγματικών αριθμών. H προσκόλληση σε αυτό του μηδέν και των αρνητικών πραγματικών αριθμών μπορεί να γίνει με τον ευρέως γνωστό κοινό τρόπο.

Θεωρούμε γνωστούς μόνο τους μη αρνητικούς ακέραιους

$\center 0, 1, 2, 3, 4, 5, 6, 7, \ldots \tag*{}$

και τους συμβολίζουμε με μικρά λατινικά γράμματα. Αυτοί οι αριθμοί, με εξαίρεση το μηδέν, ονομάζονται φυσικοί αριθμοί. Αν

μη αρνητικός ακέραιος και

φυσικός αριθμός, τότε το σύμβολο

$\left [ \dfrac{m}{n} \right ]$

συμβολίζει το ατελές πηλίκο της διαίρεσης του

με το

, δηλαδή τον μεγαλύτερο ακέραιο αριθμό

, για τον οποίο

$kn \leq m$ .

Ορισμός 1. Πραγματικός αριθμός ονομάζεται η μονότιμη συνάρτηση

$m=\phi (n)$ ,

που ορίζεται για όλους τους φυσικούς αριθμούς

, με μη αρνητικές τιμές

, η οποία ικανοποιεί τις ακόλουθες ιδιότητες:

1) Για όλους τους φυσικούς αριθμούς

$\phi (n) = \left [ \dfrac{\phi (kn)}{k} \right ]$ .

2) Για οποιονδήποτε φυσικό αριθμό

υπάρχει τέτοιος φυσικός

, ώστε

$\phi (kn) > k \phi(n)$ .

Τους θετικούς πραγματικούς αριθμούς θα τους συμβολίζουμε με μικρά ελληνικά γράμματα και το σύνολο όλων των θετικών πραγματικών αριθμών με το γράμμα $\Phi$ . Η σχέση διάταξης, η πράξη της πρόσθεσης και του πολλαπλασιασμού εισάγονται στο σύνολο $\Phi$ με τους εξής ορισμούς:

Ορισμός 2. $\phi < \psi$ συμβολίζει, ότι υπάρχει τέτοιος φυσικός αριθμός

, για τον οποίο

$\phi (n) < \psi (n)$ .

Ορισμός 3. $\phi + \psi = \chi$ συμβολίζει, ότι για όλους τους φυσικούς αριθμούς

$\chi (n) = max \left [ \dfrac{\phi (kn) +\psi(kn)}{k} \right ]$ ,

Όπου το max

εφαρμόζεται για όλους τους φυσικούς

.

Ορισμός 4. $\phi \cdot \psi = \xi$ συμβολίζει, ότι για όλους τους φυσικούς

$\chi (n) = max \left [ \dfrac{\phi (kn) \cdot \psi(k^{\prime}n)}{n \cdot k \cdot k^{\prime}} \right ]$ .

Όπου το max

εφαρμόζεται για όλους τους φυσικούς

και $k^{\prime}$ .

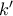Το πρόβλημα, που προτείνεται στον αναγνώστη, συμπεριλαμβάνεται στην απόδειξη το ότι το σύνολο $\Phi$ εφοδιασμένο με την παραπάνω σχέση διάταξης και τις πράξεις πρόσθεσης και πολλαπλασιασμού πράγματι διαθέτει όλες τις ιδιότητες των κοινών θετικών πραγματικών αριθμών (δηλαδή είναι ισόμορφο με το σύστημα των θετικών πραγματικών αριθμών, κατασκευασμένων με οποιοδήποτε άλλο κοινά αποδεκτό τρόπο).

Παρατήρηση 1. Για οποιονδήποτε φυσικό

η συνάρτηση

$\phi_{r}(n) = nr-1$

ικανοποιεί τις συνθήκες ορισμού του

, δηλαδή αποτελεί στην δική μας θεώρηση θετικό πραγματικό αριθμό. $^{(*)}$
Αυτός ο «αριθμός» $\phi_{r}$ μπορεί με φυσικό τρόπο να αντιστοιχηθεί με το φυσικό αριθμό

. Με αυτή την συμφωνία το σύστημα $\Phi$ γίνεται επέκταση του συστήματος των φυσικών αριθμών.

Παρατήρηση 2. Προσκολλώντας στο $\Phi$ τον αριθμό μηδέν και υποθέτοντας ότι

0+0=0

$0 \cdot 0 =0$

και για όλα τα $\phi$ του $\Phi$

$0 < \phi$ ,
$\phi +0 = 0+\phi$ ,
$\phi \cdot 0 =0 \cdot \phi$ ,

Λαμβάνουμε το σύστημα $\Phi^{\prime}$ των μη αρνητικών πραγματικών αριθμών. Το $\Phi^{\prime}$ μετά την συμφωνία που κάναμε στην παρατήρηση 1, συμπεριλαμβάνει στον εαυτό του σε μορφή υποσυνόλου, το σύνολο όλων των μη αρνητικών ακέραιων. Είναι φυσικό τώρα για οποιοδήποτε $\phi$ του $\Phi$ εξ ορισμού να θέσουμε το $\left [ \phi \right ]$ (ακέραιο μέρος του $\phi$ ) ίσο με τον μεγαλύτερο εκ των ακέραιων αριθμών, για τον οποίο

$m \leq \phi$ .

Παρατήρηση 3. Αν ορίσουμε την διαίρεση στο $\Phi^{\prime}$ ως την αντίστροφη πράξη του πολλαπλασιασμού, τότε μπορούμε να δείξουμε, ότι για οποιονδήποτε μη αρνητικό ακέραιο

και φυσικό

(θεωρώντας τους ως στοιχεία του συνόλου $\Phi^{\prime}$ ) το αποτέλεσμα της διπλής πράξης διαίρεσης και πάρσιμο του ακέραιου μέρους

$\left [ \dfrac{m}{n} \right ]$

συμπίπτει με το ατελές πηλίκο, άμεσα οριζόμενου.

Παρατήρηση 4. Τέλος, μπορούμε να αποδείξουμε ότι για οποιοδήποτε $\phi$ του $\Phi$

$\phi (n) = \phi n -1$ στην περίπτωση $\phi$ να είναι ακέραιος
$\phi (n)= \left [ \phi n \right] -1$ στην περίπτωση $\phi$ κλασματικός (μη ακέραιος).

Με τέτοιο τρόπο ο $\phi (n)$ εν τέλη προκύπτει να είναι τίποτα διαφορετικό από ότι ο μεγαλύτερος ακέραιος

, για τον οποίο

$\dfrac{m}{n} < \phi$ .

Στην φορμαλιστική θεώρηση του καινούργιου τρόπου κατασκευής του συστήματος των πραγματικών αριθμών αυτή η υπόθεση αναπόφευκτα αποτελεί τον τελικό κρίκο μιας μακράς αλυσίδας ορισμών και συμπερασμάτων εξ αυτών. Αλλά, βέβαια, αποτελεί το αρχικό σημείο για την κατανόηση της σκέψης αυτής της κατασκευής.

(*) Ο αναγνώστης εύκολα μπορεί να αντιληφθεί, ότι η συνάρτηση $f_{r}(n) =nr$ δεν ικανοποιεί την ιδιότητα 2) και για αυτό δεν συμπεριλαμβάνεται στο σύνολο $\Phi$ .

Πραγματικοί Αριθμοί Από τον Ευκλείδη στον Κολμογκόροβ

Πραγματικοί Αριθμοί Από τον Ευκλείδη στον Κολμογκόροβ

Μέλη σε σύνδεση