 ;
;Μπάμπης
Συντονιστής: ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
 ;
;Τα συγχαρητήριά μου στην κόρη σου. Πολύ ωραία η λύση της.KAKABASBASILEIOS έγραψε:Μία απάντηση από την κόρη μου που πηγαίνει Α γυμνασίου....
ΔΗΜΗΤΡΗΣ έγραψε:Θα επιχειρήσω μια απόδειξη:
Έστω ο τριψήφιος αριθμός ΧΨΩ. Αφαιρούμε από τον διψήφιο ΧΨ το Ω και βρίσκουμε αποτέλεσμα 10Χ+Ψ-Ω.
Τώρα ο αριθμός αυτός είναι πολλαπλάσιος του 11 σημαίνει ότι 10Χ+Ψ-Ω=11λ , με λ ακέραιο. Άρα Ω=10Χ+Ψ-11λ
Τώρα έχουμε: ΧΨΩ=100Χ+10Ψ+Ω=100Χ+10Ψ+10Χ+Ψ-11λ=110Χ+11Ψ-11λ=11(10Χ+Ψ-λ)
Άρα ο τριψήφιος ΧΨΩ διαιρείται με το 11.
Αν τώρα ο 10Χ+Ψ-Ω δεν είναι πολ/σιος του 11, τότε θα ισούται με 11λ+1 ή 11λ+2 ή ... ή 11λ+10
1η περ. Αν 10Χ+Ψ-Ω=11λ+1 τότε Ω=10Χ+Ψ-11λ-1
Άρα ΧΨΩ=100Χ+10Ψ+Ω=100Χ+10Ψ+10Χ+Ψ-11λ-1=110Χ+11Ψ-11λ-1=11(10Χ+Ψ-λ)-1, άρα δεν είναι πολ/σιος του 11.
Όμοια και για τις άλλες περιπτώσεις, και όμοια και για τους τετραψήφιους κλπ αριθμούς

 είναι
είναι  .
. ο αριθμός που θέλουμε να διαιρέσουμε με το 11 θα είναι
ο αριθμός που θέλουμε να διαιρέσουμε με το 11 θα είναι
 .
.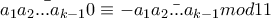 . Επειδή οι δυνάμεις του -1 είναι τώρα κατά 1 μικρότερες. Και για την προηγούμενη σχέση θα ισχύει επομένως
. Επειδή οι δυνάμεις του -1 είναι τώρα κατά 1 μικρότερες. Και για την προηγούμενη σχέση θα ισχύει επομένως Άρα και
Άρα και  δηλαδή
δηλαδή
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες