 , ο οποίος έχει
, ο οποίος έχει  ψηφία (και το
ψηφία (και το  εμφανίζεται
εμφανίζεται 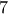 φορές.)
φορές.)Να βρεθεί το υπόλοιπο της διαίρεσης του
 ,
, (1) Με το

(2) Με το

(3) Με το

(4) Με το

(5) Με το

Συντονιστής: ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
 , ο οποίος έχει
, ο οποίος έχει  ψηφία (και το
ψηφία (και το  εμφανίζεται
εμφανίζεται 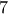 φορές.)
φορές.) ,
, 




 άρα το υπόλοιπο είναι
άρα το υπόλοιπο είναι 
 επομένως ο
επομένως ο  δηλ
δηλ  άρα το υπόλοιπο είναι 1
άρα το υπόλοιπο είναι 1 άρα είναι της μορφής
άρα είναι της μορφής  άρα το υπόλοιπο είναι
άρα το υπόλοιπο είναι 
 , με
, με . Θα δείξουμε ότι
. Θα δείξουμε ότι 
 άρα το u δεν μπορεί να είναι
άρα το u δεν μπορεί να είναι  .
.  άρα το u δεν μπορεί να είναι
άρα το u δεν μπορεί να είναι  . Τέλος θα αποκλείσουμε την περίπτωση
. Τέλος θα αποκλείσουμε την περίπτωση  αφού τότε ο
αφού τότε ο  δηλ
δηλ  δηλ της μορφής
δηλ της μορφής  κάτι που δεν γίνεται να ισχύει λόγω 2)
κάτι που δεν γίνεται να ισχύει λόγω 2)
 , είναι
, είναι 
 , (αφού το άθροισμα των ψηφίων του είναι πολλαπλάσιο του
, (αφού το άθροισμα των ψηφίων του είναι πολλαπλάσιο του  ).
). , με
, με  ακέραιο. Συνεπώς (με βάση την Ευκλείδεια διαίρεση), το υπόλοιπο της διαίρεσης του
ακέραιο. Συνεπώς (με βάση την Ευκλείδεια διαίρεση), το υπόλοιπο της διαίρεσης του  με το
με το 
 .
.
 είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  (αφού είναι άρτιος) αλλά επίσης είναι και πολλαπλάσιο
(αφού είναι άρτιος) αλλά επίσης είναι και πολλαπλάσιο , αφού το άθροισμα των ψηφίων του είναι
, αφού το άθροισμα των ψηφίων του είναι  , (και το
, (και το  είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  )
) είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  και του
και του  και αφού επί πλέον
και αφού επί πλέον και
και  είναι πρώτοι μεταξύ τους, άρα θα είναι και πολλαπλάσιο του
είναι πρώτοι μεταξύ τους, άρα θα είναι και πολλαπλάσιο του  .
. , όπου
, όπου  ακέραιος.
ακέραιος. με το
με το  είναι
είναι  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες