 τέτοιοι ώστε
τέτοιοι ώστε  .
.Να βρείτε την ελάχιστη δυνατή τιμή του
 .
.Υ.Γ. Φραγή μέχρι 2/4 στα δεινοσαυράκια (Χάρη, Διονύση, JimNt. ... )
Συντονιστής: Παύλος Μαραγκουδάκης
 τέτοιοι ώστε
τέτοιοι ώστε  .
. .
.ΑφούΟρέστης Λιγνός έγραψε:Έστωτέτοιοι ώστε
.
Να βρείτε την ελάχιστη δυνατή τιμή του.
Υ.Γ. Φραγή μέχρι 2/4 στα δεινοσαυράκια (Χάρη, Διονύση, JimNt. ... )
 και
και  , έχω ότι
, έχω ότι  τέλειο τετράγωνο. Η ελάχιστη τιμή του
τέλειο τετράγωνο. Η ελάχιστη τιμή του  , για να
, για να  το μικρότερο δυνατό τέλειο τετράγωνο, είναι
το μικρότερο δυνατό τέλειο τετράγωνο, είναι  . Άρα
. Άρα  . Άρα,
. Άρα, , είναι
, είναι 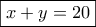
 τέτοιοι ώστε
τέτοιοι ώστε  .
. και να εξηγήσεις αναλυτικά την λύση σου.
και να εξηγήσεις αναλυτικά την λύση σου.Αναλυτικά τι εννοείς; Να το λύσω με μαθηματικές πράξεις; Εγώ το έλυσα έτσι γιατί ήταν μικρό το νούμερο. ΘαΟρέστης Λιγνός έγραψε:Nα εξηγήσεις αναλυτικά την λύση σου.
θέλει εξήγηση, όσο απλό κι αν είναι.Κατερινόπουλος Νικόλας έγραψε: Η ελάχιστη τιμή του, για να έχουμε
το μικρότερο δυνατό τέλειο τετράγωνο, είναι
.
Κατερινόπουλος Νικόλας έγραψε:Αναλυτικά τι εννοείς; Να το λύσω με μαθηματικές πράξεις; Εγώ το έλυσα έτσι γιατί ήταν μικρό το νούμερο. ΘαΟρέστης Λιγνός έγραψε:Nα εξηγήσεις αναλυτικά την λύση σου.
ξαναπροσπαθήσω και θα σου απαντήσω!
Πάνω σε αυτό δουλεύω τώρα!!!JimNt. έγραψε:Η ανάλυση σε πρώτους παράγοντες θα σε βοηθήσει


 γιατί είναι και δύο άρρητοι ενώ το
γιατί είναι και δύο άρρητοι ενώ το  γιατί είναι φυσικοί.
γιατί είναι φυσικοί.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες