 είναι μονώνυμο. Το
είναι μονώνυμο. Το  δεν είναι μονώνυμο, μια που δεν είναι ακέραια αλγεβρική παράσταση. Το
δεν είναι μονώνυμο, μια που δεν είναι ακέραια αλγεβρική παράσταση. Το  είναι μονώνυμο;
είναι μονώνυμο;Συντονιστής: Γιώργος Ρίζος
 είναι μονώνυμο. Το
είναι μονώνυμο. Το  δεν είναι μονώνυμο, μια που δεν είναι ακέραια αλγεβρική παράσταση. Το
δεν είναι μονώνυμο, μια που δεν είναι ακέραια αλγεβρική παράσταση. Το  είναι μονώνυμο;
είναι μονώνυμο; .
.Να ρισκάρω μία απάντηση;Μιχάλης Νάννος έγραψε:Τοείναι μονώνυμο. Το
δεν είναι μονώνυμο, μια που δεν είναι ακέραια αλγεβρική παράσταση. Το
είναι μονώνυμο;
 έχει βέβαια πεδίο ορισμού το
έχει βέβαια πεδίο ορισμού το  έστω κι αν μετά από πράξεις ο τύπος της μπορεί να γίνει
έστω κι αν μετά από πράξεις ο τύπος της μπορεί να γίνει 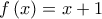
 θα έλεγα ότι εφόσον περιέχει τη δύναμη
θα έλεγα ότι εφόσον περιέχει τη δύναμη  δηλαδή το κλάσμα
δηλαδή το κλάσμα  , και πάλι δεν θα είναι μονώνυμο, έστω και αν κατόπιν πράξεων αποδεικνύεται ίση με την
, και πάλι δεν θα είναι μονώνυμο, έστω και αν κατόπιν πράξεων αποδεικνύεται ίση με την  . Δεν είναι το ίδιο πράγμα οι δύο παραστάσεις, αφού πχ δεν ορίζονται για τις ίδιες τιμές των x.
. Δεν είναι το ίδιο πράγμα οι δύο παραστάσεις, αφού πχ δεν ορίζονται για τις ίδιες τιμές των x.Καλησπέρα. Γνώμη μου είναι ότι τόσο τοΜιχάλης Νάννος έγραψε:Τοείναι μονώνυμο. Το
δεν είναι μονώνυμο, μια που δεν είναι ακέραια αλγεβρική παράσταση. Το
είναι μονώνυμο;
 όσο και το
όσο και το  είναι μονώνυμα. Το πρώτο διότι είναι ίσο με
είναι μονώνυμα. Το πρώτο διότι είναι ίσο με  (με τον περιορισμό ότι δεν έχει νόημα η αριθμητική τιμή του για χ = 0) και το δεύτερο διότι είναι ίσο με
(με τον περιορισμό ότι δεν έχει νόημα η αριθμητική τιμή του για χ = 0) και το δεύτερο διότι είναι ίσο με  με τον ίδιο περιορισμό.
με τον ίδιο περιορισμό. είναι, όταν γραφτεί
είναι, όταν γραφτεί 
 κάτι που φυσικά δεν ισχύει. Για τον ορισμό του σχολικού βιβλίου θα συμφωνήσω όμως ότι δεν είναι σαφής.
κάτι που φυσικά δεν ισχύει. Για τον ορισμό του σχολικού βιβλίου θα συμφωνήσω όμως ότι δεν είναι σαφής. είναι μονώνυμο;
είναι μονώνυμο;Όχι, η παράσταση αυτή δεν είναι μονώνυμο, αφού τοpropaid έγραψε:Θα μπορούσαμε ανάλογα να ισχυριστούμε ότι η παράστασηείναι μονώνυμο;
Γιάννης Στάμου

 είναι μονώνυμο, αφού μεταξύ των μεταβλητών της
είναι μονώνυμο, αφού μεταξύ των μεταβλητών της  , σημειώνεται μόνο η ΄πράξη του πολλαπλασιασμού.
, σημειώνεται μόνο η ΄πράξη του πολλαπλασιασμού.  θα ήταν μονώνυμο, αφού ικανοποιεί άμεσα τον ορισμό
θα ήταν μονώνυμο, αφού ικανοποιεί άμεσα τον ορισμό θα ήταν μονώνυμο, αφού μπορεί να γραφεί :
θα ήταν μονώνυμο, αφού μπορεί να γραφεί :
 , θα ήταν μονώνυμο, αφού μπορεί να γραφεί:
, θα ήταν μονώνυμο, αφού μπορεί να γραφεί: 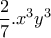 , (με
, (με 
 , είναι μονώνυμο, αφού είναι μια σταθερά.
, είναι μονώνυμο, αφού είναι μια σταθερά. », γιατί το τότε το σχολικό βιβλίο δεν συμπεριελάμβανε το
», γιατί το τότε το σχολικό βιβλίο δεν συμπεριελάμβανε το  στους φυσικούς αριθμούς).
στους φυσικούς αριθμούς). , η οποία δεν είναι εξ αρχής στην μορφή που δίνει ο ορισμός, αλλά γράφεται
, η οποία δεν είναι εξ αρχής στην μορφή που δίνει ο ορισμός, αλλά γράφεται και τώρα έχει την μορφή που θέλουμε, θα μπορούμε να πούμε ότι είναι μονώνυμο; (με
και τώρα έχει την μορφή που θέλουμε, θα μπορούμε να πούμε ότι είναι μονώνυμο; (με  )
) έχει την διαίρεση (
έχει την διαίρεση ( )οπότε δεν είναι μονώνυμο.
)οπότε δεν είναι μονώνυμο.
 και όχι
και όχι  ).
).
Με τη λογική του Κώστα (στην ουσία του ορισμού) η έκφρασηΤηλέγραφος Κώστας έγραψε:Τα μονώνυμα εκφράζουν πολλαπλασιασμό μεταξύ των μεταβλητών και όχι διαίρεση η άλλη πράξη.
Η παράστασηέχει την διαίρεση (
)οπότε δεν είναι μονώνυμο.
 δεν είναι μονώνυμο, γιατί μεταξύ των μεταβλητών παρεμβάλλεται η πρόσθεση και όχι ο πολλαπλασιασμός, ενώ σύμφωνα με την Πανεπιστημιακή αφηρημένη Άλγεβρα, όπως τεκμηριώνει πιο πάνω ο Δημήτρης, είναι μονώνυμο.
δεν είναι μονώνυμο, γιατί μεταξύ των μεταβλητών παρεμβάλλεται η πρόσθεση και όχι ο πολλαπλασιασμός, ενώ σύμφωνα με την Πανεπιστημιακή αφηρημένη Άλγεβρα, όπως τεκμηριώνει πιο πάνω ο Δημήτρης, είναι μονώνυμο. , ώστε η αλγεβρική παράσταση
, ώστε η αλγεβρική παράσταση  να είναι μονώνυμο… προϋποθέτει η άσκηση λοιπόν, πως οι δύο όροι θα προστεθούν μεταξύ τους (εξισώνοντας τους αντίστοιχους εκθέτες για να εξασφαλίσουμε ίσα κύρια μέρη) και θα μείνει ένας.
να είναι μονώνυμο… προϋποθέτει η άσκηση λοιπόν, πως οι δύο όροι θα προστεθούν μεταξύ τους (εξισώνοντας τους αντίστοιχους εκθέτες για να εξασφαλίσουμε ίσα κύρια μέρη) και θα μείνει ένας.Αγαπητέ Δημήτρη.ΔΗΜΗΤΡΗΣ έγραψε:Αντώνη, καλησπέρα.
Πολύ ωραίος ο ορισμός, που έχεις δώσει για το μονώνυμο, ο οποίος δεν αφήνει αμφιβολίες
Μένει μόνο να έχουμε μια έγκυρη διευκρίνηση, ώστε να ξεκαθαρίσει πλήρως το τοπίο για τα μονώνυμα:
Αν μια παράσταση δεν έχει εξ αρχής την μορφή που έχεις γράψει, αλλά μπορεί να τεθεί στην πιο πάνω μορφή με κάποιους ίσως περιορισμούς για τις μεταβλητές του, τότε πάντα θα είναι μονώνυμο;
Πχ, η παράσταση, η οποία δεν είναι εξ αρχής στην μορφή που δίνει ο ορισμός, αλλά γράφεται
και τώρα έχει την μορφή που θέλουμε, θα μπορούμε να πούμε ότι είναι μονώνυμο; (με
)
Θα θέλαμε την άποψή σου, για να μας λυθεί και αυτή η απορία που συχνά αντιμετωπίζουμε στην τάξη (όπως έγραψε και ο Μιχάλης) και απαντάμε κατά την γνώμη μας...
 με
με  » (δεν πρόκειται περί συναρτήσεως με δύο μεταβλητές). Γιατί ,τότε, θα έπρεπε το μονώνυμο:
» (δεν πρόκειται περί συναρτήσεως με δύο μεταβλητές). Γιατί ,τότε, θα έπρεπε το μονώνυμο:  με
με  να θεωρείται διαφορετικό από το μονώνυμο:
να θεωρείται διαφορετικό από το μονώνυμο:  , αν και έχουν τον ίδιο συντελεστή και το ίδιο κύριο ποσό. Η αλγεβρική παράσταση:
, αν και έχουν τον ίδιο συντελεστή και το ίδιο κύριο ποσό. Η αλγεβρική παράσταση:  προφανώς δεν είναι ένα μονώνυμο. Το ερώτημα είναι, επειδή ,για τις αριθμητικές τιμές, με
προφανώς δεν είναι ένα μονώνυμο. Το ερώτημα είναι, επειδή ,για τις αριθμητικές τιμές, με  , ισχύει:
, ισχύει:  και το δεύτερο μέλος είναι ένα μονώνυμο, θα μπορούσαμε να πούμε ότι και το πρώτο μέλος είναι ένα μονώνυμο; Η απάντηση είναι: Ούτε το δεύτερο μέλος είναι ένα μονώνυμο, αφού θεωρούμε
και το δεύτερο μέλος είναι ένα μονώνυμο, θα μπορούσαμε να πούμε ότι και το πρώτο μέλος είναι ένα μονώνυμο; Η απάντηση είναι: Ούτε το δεύτερο μέλος είναι ένα μονώνυμο, αφού θεωρούμε  , όπως εξηγήσαμε παραπάνω ( επαναλαμβάνω δεν πρόκειται περί συναρτήσεων).
, όπως εξηγήσαμε παραπάνω ( επαναλαμβάνω δεν πρόκειται περί συναρτήσεων).

 είναι πραγματικοί αριθμοί.
είναι πραγματικοί αριθμοί.Καλημέρα.Α.Κυριακόπουλος έγραψε:
Οι μεταβλητές σε ένα μονώνυμο μπορούν να αντικατασταθούν με ένα οποιονδήποτε πραγματικό αριθμό ( εκτός αν κάποια μεταβλητή έχει εκθέτει μηδέν, οπότε δεν μπορεί να αντικατασταθεί με το μηδέν)...
Δεν υπάρχουν περιορισμοί για τις μεταβλητές του ( εκτός από αυτή που αναφέραμε παραπάνω, όταν πρόκειται να βρούμε την αριθμητική τιμή του ).
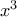 και
και 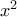 και θέλουμε να βρούμε το πηλίκο τους
και θέλουμε να βρούμε το πηλίκο τους  . Δεν πρέπει να διευκρινήσουμε ότι εφόσον το μονώνυμο
. Δεν πρέπει να διευκρινήσουμε ότι εφόσον το μονώνυμο 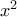 βρίσκεται στον παρονομαστή ΔΕΝ έχει νόημα η αριθμητική τιμή του για χ=0;
βρίσκεται στον παρονομαστή ΔΕΝ έχει νόημα η αριθμητική τιμή του για χ=0;nik21 έγραψε:Καλημέρα.Α.Κυριακόπουλος έγραψε:
Οι μεταβλητές σε ένα μονώνυμο μπορούν να αντικατασταθούν με ένα οποιονδήποτε πραγματικό αριθμό ( εκτός αν κάποια μεταβλητή έχει εκθέτει μηδέν, οπότε δεν μπορεί να αντικατασταθεί με το μηδέν)...
Δεν υπάρχουν περιορισμοί για τις μεταβλητές του ( εκτός από αυτή που αναφέραμε παραπάνω, όταν πρόκειται να βρούμε την αριθμητική τιμή του ).
Έχουμε τα μονώνυμακαι
και θέλουμε να βρούμε το πηλίκο τους
. Δεν πρέπει να διευκρινήσουμε ότι εφόσον το μονώνυμο
βρίσκεται στον παρονομαστή ΔΕΝ έχει νόημα η αριθμητική τιμή του για χ=0;
 , όμως το αποτέλεσμα που βρίσκουμε, δεν είναι μονώνυμο. Συμπεραίνουμε λοιπόν, ότι "μονώνυμο επί μονώνυμο είναι πάντα μονώνυμο", ενώ:
, όμως το αποτέλεσμα που βρίσκουμε, δεν είναι μονώνυμο. Συμπεραίνουμε λοιπόν, ότι "μονώνυμο επί μονώνυμο είναι πάντα μονώνυμο", ενώ: )."
)."Δεν υπάρχει λόγος να περιορίσουμε τη διαίρεση μόνο με σταθερά μονώνυμα. αν για παράδειγμα ορίσουμε ως πηλίκο της διαίρεσης ενος μονωνύμουΔΗΜΗΤΡΗΣ έγραψε:nik21 έγραψε:Καλημέρα.Α.Κυριακόπουλος έγραψε:
Οι μεταβλητές σε ένα μονώνυμο μπορούν να αντικατασταθούν με ένα οποιονδήποτε πραγματικό αριθμό ( εκτός αν κάποια μεταβλητή έχει εκθέτει μηδέν, οπότε δεν μπορεί να αντικατασταθεί με το μηδέν)...
Δεν υπάρχουν περιορισμοί για τις μεταβλητές του ( εκτός από αυτή που αναφέραμε παραπάνω, όταν πρόκειται να βρούμε την αριθμητική τιμή του ).
Έχουμε τα μονώνυμακαι
και θέλουμε να βρούμε το πηλίκο τους
. Δεν πρέπει να διευκρινήσουμε ότι εφόσον το μονώνυμο
βρίσκεται στον παρονομαστή ΔΕΝ έχει νόημα η αριθμητική τιμή του για χ=0;
Mε βάση την διευκρίνηση που ΄μας δόθηκε από Αντώνη, ναι, θα πρέπει να θέσουμε, όμως το αποτέλεσμα που βρίσκουμε, δεν είναι μονώνυμο. Συμπεραίνουμε λοιπόν, ότι "μονώνυμο επί μονώνυμο είναι πάντα μονώνυμο", ενώ:
"μονώνυμο διά μονώνυμο, δεν είναι μονώνυμο, εκτός αν ο παρονομαστής, είναι το σταθερό μονώνυμο ()."
Μετά την παρέμβαση του Αντώνη Κυριακόπουλου, νομίζω ότι οι έννοιες τακτοποιήθηκαν και καλό είναι να αναφερθούν κάποτε και στα σχολικά βιβλία, ώστε να μην υπάρχει η σύγχιση που κάθε χρόνο αντιμετωπίζουμε...
 με ένα μονώνυμο
με ένα μονώνυμο  να είναι το μονώνυμο
να είναι το μονώνυμο  (αν φυσικά υπάρχει) τέτοιο ώστε
(αν φυσικά υπάρχει) τέτοιο ώστε  , δεν υπάρχει πρόβλημα να γράψεις τη διαίρεση
, δεν υπάρχει πρόβλημα να γράψεις τη διαίρεση 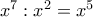
 ή ακόμα
ή ακόμα 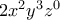 ;
; από το ''σύνολο ορισμού'' τους.Θα μου πείτε και τι έγινε !
από το ''σύνολο ορισμού'' τους.Θα μου πείτε και τι έγινε ! το αποτέλεσμα ορίζεται για όλες τις τιμές των μεταβλητών,θα πρέπει κανονικά να εξαιρεθεί η τιμή
το αποτέλεσμα ορίζεται για όλες τις τιμές των μεταβλητών,θα πρέπει κανονικά να εξαιρεθεί η τιμή  .Τι νόημα έχει λοιπόν να διατηρήσουμε στο δεύτερο μονώνυμο τη μεταβλητη
.Τι νόημα έχει λοιπόν να διατηρήσουμε στο δεύτερο μονώνυμο τη μεταβλητη  ; Φαίνεται ότι σε σχολικό επίπεδο τουλάχιστον, μόνο πρόβλημα δημιουργεί !
; Φαίνεται ότι σε σχολικό επίπεδο τουλάχιστον, μόνο πρόβλημα δημιουργεί !  τι θα πούμε ; Είναι μονώνυμο ή όχι και τι τιμές μπορεί να πάρουν οι μεταβλητές της ; Προφανώς γράφεται στη μορφή
τι θα πούμε ; Είναι μονώνυμο ή όχι και τι τιμές μπορεί να πάρουν οι μεταβλητές της ; Προφανώς γράφεται στη μορφή  και είναι μονώνυμο με τον τωρινό ορισμό ,αλλά το πεδίο ορισμού αλλάζει ! Θα πει κάποιος ότι αυτό γίνεται και στις συναρτήσεις (
και είναι μονώνυμο με τον τωρινό ορισμό ,αλλά το πεδίο ορισμού αλλάζει ! Θα πει κάποιος ότι αυτό γίνεται και στις συναρτήσεις ( ), αλλά εκεί όλα γίνονται με τάξη και συστηματικά .
), αλλά εκεί όλα γίνονται με τάξη και συστηματικά . Καλησπέρα.tsaknakis έγραψε:Δεν υπάρχει λόγος να περιορίσουμε τη διαίρεση μόνο με σταθερά μονώνυμα. αν για παράδειγμα ορίσουμε ως πηλίκο της διαίρεσης ενος μονωνύμουμε ένα μονώνυμο
να είναι το μονώνυμο
(αν φυσικά υπάρχει) τέτοιο ώστε
, δεν υπάρχει πρόβλημα να γράψεις τη διαίρεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες