
Παραγοντοποίηση
Συντονιστής: Γιώργος Ρίζος
-
Παύλος Μαραγκουδάκης
- Επιμελητής
- Δημοσιεύσεις: 1513
- Εγγραφή: Παρ Ιαν 30, 2009 1:45 pm
- Τοποθεσία: Πειραιάς
- Επικοινωνία:
Παραγοντοποίηση
Να παραγοντοποιήσετε το πολυώνυμο 

Στάλα τη στάλα το νερό το μάρμαρο τρυπά το,
εκείνο που μισεί κανείς γυρίζει κι αγαπά το.
εκείνο που μισεί κανείς γυρίζει κι αγαπά το.
Λέξεις Κλειδιά:
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13275
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Παραγοντοποίηση
Μία λύση στα όρια του ακροβατισμού. Θα υπάρχει φαντάζομαι πιο λογική αντιμετώπιση.



![\displaystyle {({x^4} + {y^4} + 50{x^2}{y^2})^2} - {[10xy({x^2} - {y^2})]^2} = \displaystyle {({x^4} + {y^4} + 50{x^2}{y^2})^2} - {[10xy({x^2} - {y^2})]^2} =](/forum/ext/geomar/texintegr/latexrender/pictures/8b9514e7df42411b418295327fb923b5.png)

Απορία: Πώς μπορούμε να πείσουμε ένα μαθητή ότι ολοκληρώθηκε (αν ολοκληρώθηκε) η παραγοντοποίηση;
-
Παύλος Μαραγκουδάκης
- Επιμελητής
- Δημοσιεύσεις: 1513
- Εγγραφή: Παρ Ιαν 30, 2009 1:45 pm
- Τοποθεσία: Πειραιάς
- Επικοινωνία:
Re: Παραγοντοποίηση
Γιώργο δεν έχω κάτι καλύτερο κατά νου. Όσο για την απορία που διατυπώνεις, έχεις δίκιο. Μια εναλλακτική διατύπωση που θα μπορούσε να σταθεί είναι:
Να αναλύσετε σε γινόμενο δύο παραγόντων 4ου βαθμού το πολυώνυμο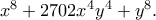
Η ιδέα είναι από ένα παλιό καλό βιβλίο του Μανόλη Μαραγκάκη "Αλγεβρικά Θέματα''.
Να αναλύσετε σε γινόμενο δύο παραγόντων 4ου βαθμού το πολυώνυμο
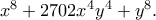
Η ιδέα είναι από ένα παλιό καλό βιβλίο του Μανόλη Μαραγκάκη "Αλγεβρικά Θέματα''.
Στάλα τη στάλα το νερό το μάρμαρο τρυπά το,
εκείνο που μισεί κανείς γυρίζει κι αγαπά το.
εκείνο που μισεί κανείς γυρίζει κι αγαπά το.
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13275
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Παραγοντοποίηση
Καλημέρα Παύλο!
Στο τρέχον βιβλίο της Γ' Γυμνασίου εφαρμόζεται η διαφορά τετραγώνων και σε αριθμούς που δεν είναι τέλεια τετράγωνα. Το
παράδειγμα του βιβλίου είναι Εδώ, θα ήθελα να εκφράσω άλλη μια απορία. Ένας μαθητής γράφει:
Εδώ, θα ήθελα να εκφράσω άλλη μια απορία. Ένας μαθητής γράφει:

![\displaystyle {({x^4} + 1351{y^4})^2} - {(780\sqrt 3 {y^4})^2} = \left[ {{x^4} + (1351 - 780\sqrt 3 ){y^4}} \right]\left[ {{x^4} + (1351 + 780\sqrt 3 ){y^4}} \right] \displaystyle {({x^4} + 1351{y^4})^2} - {(780\sqrt 3 {y^4})^2} = \left[ {{x^4} + (1351 - 780\sqrt 3 ){y^4}} \right]\left[ {{x^4} + (1351 + 780\sqrt 3 ){y^4}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/7d079c15be38e76dd707c114e56344e9.png)
Τι θα λέγαμε σ' αυτό το μαθητή;
Στο τρέχον βιβλίο της Γ' Γυμνασίου εφαρμόζεται η διαφορά τετραγώνων και σε αριθμούς που δεν είναι τέλεια τετράγωνα. Το
παράδειγμα του βιβλίου είναι
 Εδώ, θα ήθελα να εκφράσω άλλη μια απορία. Ένας μαθητής γράφει:
Εδώ, θα ήθελα να εκφράσω άλλη μια απορία. Ένας μαθητής γράφει:
![\displaystyle {({x^4} + 1351{y^4})^2} - {(780\sqrt 3 {y^4})^2} = \left[ {{x^4} + (1351 - 780\sqrt 3 ){y^4}} \right]\left[ {{x^4} + (1351 + 780\sqrt 3 ){y^4}} \right] \displaystyle {({x^4} + 1351{y^4})^2} - {(780\sqrt 3 {y^4})^2} = \left[ {{x^4} + (1351 - 780\sqrt 3 ){y^4}} \right]\left[ {{x^4} + (1351 + 780\sqrt 3 ){y^4}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/7d079c15be38e76dd707c114e56344e9.png)
Τι θα λέγαμε σ' αυτό το μαθητή;
-
Παύλος Μαραγκουδάκης
- Επιμελητής
- Δημοσιεύσεις: 1513
- Εγγραφή: Παρ Ιαν 30, 2009 1:45 pm
- Τοποθεσία: Πειραιάς
- Επικοινωνία:
Re: Παραγοντοποίηση
Πολύ καλή η παρατήρηση σου Γιώργο. Έτσι όπως μπήκε η ερώτηση, η απάντηση αυτή δεν μπορεί παρά να είναι δεκτή.
Η απάντηση δεν είναι μονοσήμαντη και μπορούμε να φτιάξουμε εύκολα τέτοια παραδείγματα όπως το πολυώνυμο
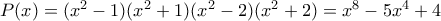
γράφεται αλλά και
αλλά και  όπως και
όπως και 
Η απάντηση δεν είναι μονοσήμαντη και μπορούμε να φτιάξουμε εύκολα τέτοια παραδείγματα όπως το πολυώνυμο
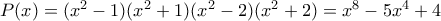
γράφεται
 αλλά και
αλλά και  όπως και
όπως και 
Στάλα τη στάλα το νερό το μάρμαρο τρυπά το,
εκείνο που μισεί κανείς γυρίζει κι αγαπά το.
εκείνο που μισεί κανείς γυρίζει κι αγαπά το.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες
