1. Το γινόμενο 3 διαδοχικών ακεραίων αριθμών διαιρείται πάντα με το 3.
2. Το γινόμενο ν διαδοχικών ακεραίων αριθμών διαιρείται πάντα με το ν.
3. Κάθε πρώτος αριθμός διάφορος του 2 και του 3 έχει δίπλα του ένα πολλαπλάσιο του 6(δύο αποδείξεις).
4. Κάθε πρώτος αριθμός διάφορος του 2 «ακουμπάει» σε ένα πολλαπλάσιο του 4.
Πρόταση 1
Το γινόμενο 3 διαδοχικών ακεραίων αριθμών διαιρείται πάντα με το 3.
Απόδειξη
Έστω
 τρεις διαδοχικοί ακέραιοι και
τρεις διαδοχικοί ακέραιοι και  το γινόμενό τους. Διαιρώντας τον
το γινόμενό τους. Διαιρώντας τον  με το 3 έχω
με το 3 έχω  , με
, με  .
.Υπάρχουν οι εξής περιπτώσεις:
Αν
 τότε
τότε  .
.Αν
 τότε
τότε  .
.Αν
 τότε
τότε  .
.Πρόταση 2
Το γινόμενο
 διαδοχικών ακεραίων αριθμών διαιρείται πάντα με το
διαδοχικών ακεραίων αριθμών διαιρείται πάντα με το  .
.Απόδειξη
Έστω
 διαδοχικοί ακέραιοι πλήθους
διαδοχικοί ακέραιοι πλήθους  και
και  το γινόμενό τους. Διαιρώντας τον
το γινόμενό τους. Διαιρώντας τον  με το
με το  έχω
έχω  , με
, με  .
.Αν
 τότε
τότε  . Σε κάθε άλλη περίπτωση, όποια και αν είναι η τιμή του
. Σε κάθε άλλη περίπτωση, όποια και αν είναι η τιμή του  , στο γινόμενο
, στο γινόμενο  υπάρχει όρος της μορφής
υπάρχει όρος της μορφής  , ο οποίος με αντικατάσταση του
, ο οποίος με αντικατάσταση του  γίνεται
γίνεται  , ο οποίος διαιρείται με το
, ο οποίος διαιρείται με το  , άρα και το γινόμενο
, άρα και το γινόμενο  διαιρείται με το
διαιρείται με το  .
.Πρόταση 3
Κάθε πρώτος αριθμός διάφορος του 2 και του 3 έχει δίπλα του ένα πολλαπλάσιο του 6.
Απόδειξη 1
Έστω
 πρώτος με
πρώτος με  και
και  .
.Ο
 διαιρούμενος δια 6, δίνει υπόλοιπο
διαιρούμενος δια 6, δίνει υπόλοιπο  και πηλίκο
και πηλίκο  , άρα
, άρα  .
.Εξετάζουμε τις περιπτώσεις:
 : αποκλείεται γιατί ο
: αποκλείεται γιατί ο  είναι πρώτος.
είναι πρώτος. :αποκλείεται γιατί ο
:αποκλείεται γιατί ο  είναι πρώτος.
είναι πρώτος. :αποκλείεται γιατί ο
:αποκλείεται γιατί ο  είναι πρώτος.
είναι πρώτος. :αποκλείεται γιατί ο
:αποκλείεται γιατί ο  είναι πρώτος.
είναι πρώτος.Άρα
 ή
ή  , το οποίο σημαίνει ότι το
, το οποίο σημαίνει ότι το  ή το
ή το  είναι πολλαπλάσιο του 6.
είναι πολλαπλάσιο του 6.Δηλαδή σε κάθε περίπτωση είτε ο αριστερός είτε ο δεξιός γείτονας του
 είναι πολλαπλάσιο του 6.
είναι πολλαπλάσιο του 6.Απόδειξη 2
Έστω
 πρώτος και
πρώτος και  τέτοιος ώστε
τέτοιος ώστε  , δηλαδή ο
, δηλαδή ο  βρίσκεται ανάμεσα σε 2 διαδοχικούς άρτιους αριθμούς. Τα
βρίσκεται ανάμεσα σε 2 διαδοχικούς άρτιους αριθμούς. Τα  είναι τρεις διαδοχικοί αριθμοί, άρα σύμφωνα με την πρόταση 1, το γινόμενό τους διαιρείται με το 3.
είναι τρεις διαδοχικοί αριθμοί, άρα σύμφωνα με την πρόταση 1, το γινόμενό τους διαιρείται με το 3.Ο
 δεν μπορεί να διαιρείται με το 3, θα διαιρείται ένας εκ των δύο άρτιων αριθμών
δεν μπορεί να διαιρείται με το 3, θα διαιρείται ένας εκ των δύο άρτιων αριθμών 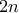 ,
,  . Τότε αυτός διαιρείται και με το 2 και με το 3, επομένως διαιρείται και με το 6, δηλαδή ο
. Τότε αυτός διαιρείται και με το 2 και με το 3, επομένως διαιρείται και με το 6, δηλαδή ο  "ακουμπά" σε ένα πολλαπλάσιο του 6.
"ακουμπά" σε ένα πολλαπλάσιο του 6.Πρόταση 4
Κάθε πρώτος αριθμός
 "ακουμπάει" σε ένα πολλαπλάσιο του 4.
"ακουμπάει" σε ένα πολλαπλάσιο του 4.Απόδειξη
Έστω
 πρώτος αριθμός, με
πρώτος αριθμός, με  . Ο
. Ο  διαιρούμενος δια 4, δίνει υπόλοιπο
διαιρούμενος δια 4, δίνει υπόλοιπο  και πηλίκο
και πηλίκο  , άρα
, άρα  .
.Εξετάζουμε τις περιπτώσεις:
 : αποκλείεται γιατί ο
: αποκλείεται γιατί ο  είναι πρώτος.
είναι πρώτος. :αποκλείεται γιατί ο
:αποκλείεται γιατί ο  είναι πρώτος.
είναι πρώτος.Άρα
 ή
ή  , το οποίο σημαίνει ότι το
, το οποίο σημαίνει ότι το  ή το
ή το  είναι πολλαπλάσιο του 4.
είναι πολλαπλάσιο του 4.Δηλαδή σε κάθε περίπτωση είτε ο αριστερός είτε ο δεξιός γείτονας του
 είναι πολλαπλάσιο του 4.
είναι πολλαπλάσιο του 4.π.χ 16<17<18, 18<19<20
Παρατήρηση
Η πρόταση αυτή αποδεικνύεται και με δεύτερο τρόπο, αν αποδείξουμε με Μαθηματική Επαγωγή ότι στη σχέση
 για κάθε
για κάθε  , ένα εκ των
, ένα εκ των  είναι πολλαπλάσιο του 4.
είναι πολλαπλάσιο του 4.
 . Άρα και το γινόμενό τους είναι πολλαπλάσιο του
. Άρα και το γινόμενό τους είναι πολλαπλάσιο του 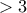 είναι περιττοί και άρα της μορφής
είναι περιττοί και άρα της μορφής  ή
ή  . Η περίπτωση
. Η περίπτωση  .
.  . Aυτοί έχουν δίπλα τους (και οι δύο) τον
. Aυτοί έχουν δίπλα τους (και οι δύο) τον  .
. διαιρεί το γινόμενο
διαιρεί το γινόμενο 
 ) ότι το γινόμενο πέντε διαδοχικών φυσικών διαιρείται με το
) ότι το γινόμενο πέντε διαδοχικών φυσικών διαιρείται με το  , αλλά τώρα αυτό βελτιώνεται στο ότι διαιρείται με το
, αλλά τώρα αυτό βελτιώνεται στο ότι διαιρείται με το  .
.