
- diplos topos 2.png (39.97 KiB) Προβλήθηκε 441 φορές
Για τον τόπο του

, μόνο τα βήματα γιατί οι πράξεις είναι απαγορευτικές.
Έστω

οι συντεταγμένες του τυπικού σημείου. Μπορούμε τότε να βρούμε τις συντεταγμένες του

. Θα βγει

από όπου μπορούμε να βρούμε τα μήκη

. Οι παραστάσεις είναι μεγάλες, αλλά θέμα ρουτίνας (δεν το κάνω).
Τώρα η συνήκη του εμβαδού γράφεται

, δηλαδή

, ισοδύναμα

.
Αυτός είναι ο ζητούμενος τόπος, σε πεπλεγμένη μορφή.
Είναι ευκολότερο να είχα εργαστεί με πολικές συντεταγμένες, αλλά το θεώρησα έξω από τις γνώσεις των μαθητών, και δυσανάλογο με το πρώτο μέρος της άσκησης.
Η εικόνα παραπάνω είναι Print Screen του τόπου, όπως την σχεδίασε ένα λογισμικό.
 είναι σταθερό σημείο του κύκλου
είναι σταθερό σημείο του κύκλου  , ενώ το
, ενώ το  κινείται σ' αυτόν . Με βάση την χορδή
κινείται σ' αυτόν . Με βάση την χορδή , σχεδιάζουμε το ορθογώνιο
, σχεδιάζουμε το ορθογώνιο  , εμβαδού
, εμβαδού 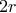 τετραγωνικών μονάδων .
τετραγωνικών μονάδων .  . Αν σας φάνηκα δύσκολο , βρείτε και τον γεωμετρικό του
. Αν σας φάνηκα δύσκολο , βρείτε και τον γεωμετρικό του  .
. μέχρι να τμήσει την διάμετρο. Δεδομένου ότι
μέχρι να τμήσει την διάμετρο. Δεδομένου ότι  , η προέκταση αυτή θα περάσει από το αριστερό άκρο
, η προέκταση αυτή θα περάσει από το αριστερό άκρο  της διαμέτρου. Φέρνουμε τώρα την κάθετη
της διαμέτρου. Φέρνουμε τώρα την κάθετη  .
.  έχουμε
έχουμε  . Άρα
. Άρα  (σταθερό). Συνεπώς το
(σταθερό). Συνεπώς το  πάνω από την διάμετρο. Την κόκκινη. Λεπτομερέστερα, διαγράφει την δεξιά ημιευθεία καθώς το
πάνω από την διάμετρο. Την κόκκινη. Λεπτομερέστερα, διαγράφει την δεξιά ημιευθεία καθώς το  οι συντεταγμένες του τυπικού σημείου. Μπορούμε τότε να βρούμε τις συντεταγμένες του
οι συντεταγμένες του τυπικού σημείου. Μπορούμε τότε να βρούμε τις συντεταγμένες του  από όπου μπορούμε να βρούμε τα μήκη
από όπου μπορούμε να βρούμε τα μήκη  . Οι παραστάσεις είναι μεγάλες, αλλά θέμα ρουτίνας (δεν το κάνω).
. Οι παραστάσεις είναι μεγάλες, αλλά θέμα ρουτίνας (δεν το κάνω). , δηλαδή
, δηλαδή  , ισοδύναμα
, ισοδύναμα  .
. της διαμέτρου. Οι συντεταγμένες του
της διαμέτρου. Οι συντεταγμένες του  , αλλά αλλάζω το σύμβολο της ακτίνας του κύκλου σε
, αλλά αλλάζω το σύμβολο της ακτίνας του κύκλου σε  για να μην έχουμε το
για να μην έχουμε το  με δύο έννοιες.
με δύο έννοιες.  , ισοδύναμα
, ισοδύναμα  , άρα
, άρα 

 και με χρήση των
και με χρήση των  έχουμε
έχουμε  οπότε
οπότε  , ισοδύναμα
, ισοδύναμα 