 και
και  να βρεθεί
να βρεθεί ο μικρότερος θετικός ακέραιος
 για τον οποίο ο
για τον οποίο ο  τελειώνει σε
τελειώνει σε  μηδενικά.
μηδενικά.Ευθύμης
Συντονιστής: Γιώργος Ρίζος
 και
και  να βρεθεί
να βρεθεί  για τον οποίο ο
για τον οποίο ο  τελειώνει σε
τελειώνει σε  μηδενικά.
μηδενικά. επιβεβαιώνεται με υπολογιστή ελέγχοντας όλους τους αριθμούς Fibonacci μέχρι να βρεθεί κάποιος που να τελειώνει σε τέσσερα μηδενικά.
επιβεβαιώνεται με υπολογιστή ελέγχοντας όλους τους αριθμούς Fibonacci μέχρι να βρεθεί κάποιος που να τελειώνει σε τέσσερα μηδενικά.Κώδικας: Επιλογή όλων
v=[0,1]
i=1
while (v[i]%10000 != 0):
i=i+1
v.append(v[i-1]+v[i-2])
print i
 και
και  να βρεθεί ο μικρότερος θετικός ακέραιος
να βρεθεί ο μικρότερος θετικός ακέραιος  για τον οποίο ο
για τον οποίο ο  τελειώνει σε:
τελειώνει σε: μηδενικό. β)
μηδενικό. β)  μηδενικά.
μηδενικά.Ενδιαφέρον.Demetres έγραψε:υπάρχει αριθμός Fibonacci ο οποίος λήγει σε τέσσερα μηδενικά. (Το αφήνω ως άσκηση.)
 για τον
για τον  (ή όσα μηδένικά θέλουμε).
(ή όσα μηδένικά θέλουμε). 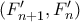 υπάρχουν
υπάρχουν  με
με 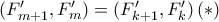 . Έπεται
. Έπεται  και άρα
και άρα  (χρησιμοποίησα την ιδιότητα
(χρησιμοποίησα την ιδιότητα  .
. , που είναι σαν την
, που είναι σαν την  αλλά "μία μονάδα πιο κάτω".
αλλά "μία μονάδα πιο κάτω".  και άρα
και άρα  οπότε και
οπότε και  , που είναι το ζητούμενο.
, που είναι το ζητούμενο.Ναι, υπάρχει τρόπος να βρεθεί οDemetres έγραψε:
Για την εύρεση του μικρότερου τέτοιου αριθμού θα ήθελα όντως να δω λύση κατάλληλη (*) για αυτόν τον φάκελο.
(*) Δηλαδή και με λίγες πράξεις αλλά και χωρίς πολλή αριθμοθεωρία.
 για τον οποίο ο αντίστοιχος
για τον οποίο ο αντίστοιχος  είναι
είναι  , που πράγματι είναι ο
, που πράγματι είναι ο  , με ελάχιστες και σχετικά εύκολες πράξεις και με χρήση μιας ιδιότητας των αριθμών Φιμπονάτσι.
, με ελάχιστες και σχετικά εύκολες πράξεις και με χρήση μιας ιδιότητας των αριθμών Φιμπονάτσι. για τον οποίο ο
για τον οποίο ο  τελειώνει:
τελειώνει:  μηδενικό β) σε
μηδενικό β) σε  γ) σε
γ) σε  δ) σε
δ) σε  μηδενικά.
μηδενικά. κάποιος ακέραιος αριθμός.
κάποιος ακέραιος αριθμός. O μικρότερος πολλαπλάσιος του
O μικρότερος πολλαπλάσιος του  αριθμός είναι ο
αριθμός είναι ο  και του
και του  είναι ο
είναι ο 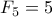 , οπότε ο μικρότερος
, οπότε ο μικρότερος  είναι ο
είναι ο 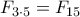 και πράγματι στον πίνακα των αριθμών Φιμπονάτσι βλέπω
και πράγματι στον πίνακα των αριθμών Φιμπονάτσι βλέπω  και δεν υπάρχει μικρότερος
και δεν υπάρχει μικρότερος  από αυτόν.
από αυτόν. . Ο μικρότερος πολλαπλάσιος του
. Ο μικρότερος πολλαπλάσιος του 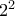 είναι ο
είναι ο  και ο μικρότερος πολλαπλάσιος του
και ο μικρότερος πολλαπλάσιος του  είναι, φυσικά, ο
είναι, φυσικά, ο  , άρα ο ζητούμενος αριθμός είναι ο
, άρα ο ζητούμενος αριθμός είναι ο  και πράγματι στον πίνακα βλέπω:
και πράγματι στον πίνακα βλέπω:  και δεν υπάρχει μικρότερος από αυτόν αριθμός
και δεν υπάρχει μικρότερος από αυτόν αριθμός 
 το οποίο θα το χρησιμοποιήσουμε αμέσως παρακάτω.)
το οποίο θα το χρησιμοποιήσουμε αμέσως παρακάτω.) Για το
Για το  πάλι ο
πάλι ο  (το
(το  που μας περίσσεψε από πριν, το χρησιμοποιούμε τώρα) και ο μικρότερος
που μας περίσσεψε από πριν, το χρησιμοποιούμε τώρα) και ο μικρότερος 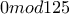 είναι ο
είναι ο  , άρα ο ζητούμενος αριθμός είναι ο
, άρα ο ζητούμενος αριθμός είναι ο 
 . Ο μικρότερος
. Ο μικρότερος  είναι ο
είναι ο 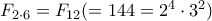 και ο μικρότερος
και ο μικρότερος  είναι ο
είναι ο  , άρα ο μικρότερος
, άρα ο μικρότερος  είναι ο
είναι ο 
 και εικάζω ότι αυτή η σχέση, η προσθήκη μηδενικών ένθεν και ένθεν της ισοδυναμίας, μπορεί να μην έχει τελειωμό.
και εικάζω ότι αυτή η σχέση, η προσθήκη μηδενικών ένθεν και ένθεν της ισοδυναμίας, μπορεί να μην έχει τελειωμό. του κ. Ρωμανίδη. Το έθεσε ο Γιώργος Ριζόπουλος και το έλυσε ο Θανάσης Παπαδημητρίου (papadim), συνάδελφοι Πολιτικοί μηχανικοί ΕΜΠ.
του κ. Ρωμανίδη. Το έθεσε ο Γιώργος Ριζόπουλος και το έλυσε ο Θανάσης Παπαδημητρίου (papadim), συνάδελφοι Πολιτικοί μηχανικοί ΕΜΠ. ισχύει μόνο όταν
ισχύει μόνο όταν  πρώτοι μεταξύ τους. (Π.χ. Το
πρώτοι μεταξύ τους. (Π.χ. Το  δεν είναι πολλαπλάσιο του
δεν είναι πολλαπλάσιο του  .)
.) 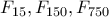 και
και  λήγουν σε
λήγουν σε  και
και  μηδενικά αντίστοιχα το κριτήριο εφαρμόζεται σε σχετικά πρώτους αριθμούς οπότε δεν υπάρχει πρόβλημα σε αυτήν την εφαρμογή.
μηδενικά αντίστοιχα το κριτήριο εφαρμόζεται σε σχετικά πρώτους αριθμούς οπότε δεν υπάρχει πρόβλημα σε αυτήν την εφαρμογή. π.χ. να μην λήγει σε
π.χ. να μην λήγει σε  μηδενικά; Το πιο πάνω κριτήριο δεν είναι ικανό να μας απαντήσει αυτό το ερώτημα.
μηδενικά; Το πιο πάνω κριτήριο δεν είναι ικανό να μας απαντήσει αυτό το ερώτημα.  .
. . Άρα το
. Άρα το  δεν είναι πολλαπλάσιο του
δεν είναι πολλαπλάσιο του  και άρα δεν μπορεί να λήγει σε τέσσερα μηδενικά.
και άρα δεν μπορεί να λήγει σε τέσσερα μηδενικά. είναι ο μικρότερος αριθμός Fibonacci ο οποίος λήγει σε τέσσερα μηδενικά αρκεί προηγουμένως να δείξουμε ότι ο
είναι ο μικρότερος αριθμός Fibonacci ο οποίος λήγει σε τέσσερα μηδενικά αρκεί προηγουμένως να δείξουμε ότι ο  είναι ο μικρότερος που είναι πολλαπλάσιο του
είναι ο μικρότερος που είναι πολλαπλάσιο του 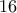 (απλές πράξεις) και ο
(απλές πράξεις) και ο  είναι ο μικρότερος που είναι πολλαπλάσιο του
είναι ο μικρότερος που είναι πολλαπλάσιο του  . Για το τελευταίο τα πιο πάνω κριτήρια δεν επαρκούν και είτε πρέπει να κάνουμε τις πράξεις, είτε να βρούμε κάποιο επιπλέον κριτήριο αν θέλουμε να τις αποφύγουμε.
. Για το τελευταίο τα πιο πάνω κριτήρια δεν επαρκούν και είτε πρέπει να κάνουμε τις πράξεις, είτε να βρούμε κάποιο επιπλέον κριτήριο αν θέλουμε να τις αποφύγουμε.Σύμφωνα με τον συλλογισμό, το γινόμενο των μικρότερων πολλαπλασίωνealexiou έγραψε:κάποιος ακέραιος αριθμός.
α)O μικρότερος πολλαπλάσιος του
αριθμός είναι ο
και του
είναι ο
, οπότε ο μικρότερος
είναι ο
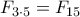
....
Πηγή: Το θέμα είναι από τοτου κ. Ρωμανίδη. Το έθεσε ο Γιώργος Ριζόπουλος και το έλυσε ο Θανάσης Παπαδημητρίου (papadim), συνάδελφοι Πολιτικοί μηχανικοί ΕΜΠ.
 των
των  οδηγεί μέσω του
οδηγεί μέσω του  σε μικρότερο πολλαπλάσιο του
σε μικρότερο πολλαπλάσιο του  . Χμμμμμ, και το
. Χμμμμμ, και το  στο
στο  που πήγε; Αν έχει και αυτό δεκάρι μέσα του, τότε χάσαμε το ελάχιστο μια και βρεθήκαμε στο
που πήγε; Αν έχει και αυτό δεκάρι μέσα του, τότε χάσαμε το ελάχιστο μια και βρεθήκαμε στο  . Με άλλα λόγια η όποια απόδειξη πρέπει να λάβει υπόψη και το
. Με άλλα λόγια η όποια απόδειξη πρέπει να λάβει υπόψη και το  (στο συγκεκριμένο θέμα, η απόδειξη φτιάχνει).
(στο συγκεκριμένο θέμα, η απόδειξη φτιάχνει). Σωστά. Μου ξέφυγε, καθώς είχα στο μυαλό μου ότι το κριτήριο εφαρμόσθηκε σε σχετικά πρώτους αριθμούς, αλλά το σωστό σωστό και διορθώνω σε αυτό που ήθελα και και κυρίως έπρεπε να γράψω "Demetres έγραψε:Το κριτήριοισχύει μόνο όταν
πρώτοι μεταξύ τους.
 και αν
και αν  πρώτοι μεταξύ τους τότε
πρώτοι μεταξύ τους τότε  "
"Δεν νομίζω ότι υπάρχει πρόβλημα γιατί αφού ξέρουμε ότι οDemetres έγραψε:
Υπάρχει όμως πρόβλημα αλλού. Γιατί τοπ.χ. να μην λήγει σε
μηδενικά; Το πιο πάνω κριτήριο δεν είναι ικανό να μας απαντήσει αυτό το ερώτημα.
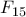 είναι ο μικρότερος αριθμός Φιμπονάτσι
είναι ο μικρότερος αριθμός Φιμπονάτσι  και με βάση την ιδιότητα ότι αν ο αριθμός
και με βάση την ιδιότητα ότι αν ο αριθμός  διαιρεί τον αριθμό
διαιρεί τον αριθμό  τότε και ο αριθμός
τότε και ο αριθμός  διαιρεί τον αριθμό
διαιρεί τον αριθμό  και το αντίστροφο (Δεν έχω απόδειξη, αλλά μην ξεχνάμε ότι είμαστε στον φάκελλο Διασκεδαστικά Μαθηματικά, και γιαυτό το έβαλα εδώ)
και το αντίστροφο (Δεν έχω απόδειξη, αλλά μην ξεχνάμε ότι είμαστε στον φάκελλο Διασκεδαστικά Μαθηματικά, και γιαυτό το έβαλα εδώ) έχουμε
έχουμε  , άρα επειδή ο
, άρα επειδή ο  δεν διαιρεί τον
δεν διαιρεί τον  και ο
και ο 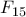 δεν διαιρεί τον
δεν διαιρεί τον  , δηλαδή ο
, δηλαδή ο  δεν έχει όχι
δεν έχει όχι  μηδενικά αλλά ούτε ένα μηδενικό στο τέλος και πράγματι επιβεβαιώνεται από το λογισμικό.
μηδενικά αλλά ούτε ένα μηδενικό στο τέλος και πράγματι επιβεβαιώνεται από το λογισμικό. μηδενικά στο τέλος, διαιρούμε τον αριθμό με το
μηδενικά στο τέλος, διαιρούμε τον αριθμό με το  αντίστοιχα και ανάλογα με το αποτέλεσμα βγάζουμε συμπέρασμα π.χ ο
αντίστοιχα και ανάλογα με το αποτέλεσμα βγάζουμε συμπέρασμα π.χ ο  έχει μόνο ένα μηδενικό στο τέλος, αφού o
έχει μόνο ένα μηδενικό στο τέλος, αφού o  διαιρείται από τον
διαιρείται από τον  αλλά όχι από τον
αλλά όχι από τον 
 μηδενικά στο τέλος είναι ο
μηδενικά στο τέλος είναι ο  ή με τις κατάλληλες διαιρέσεις να βρίσκουμε αν υπάρχουν μηδενικά στο τέλος και πόσα και πάντα στα πλαίσια του φακέλλου χωρίς απολυτότητα στην τεκμηρίωση (η χρήση πινάκων αριθμών Φιμπονάτσι πχ ότι
ή με τις κατάλληλες διαιρέσεις να βρίσκουμε αν υπάρχουν μηδενικά στο τέλος και πόσα και πάντα στα πλαίσια του φακέλλου χωρίς απολυτότητα στην τεκμηρίωση (η χρήση πινάκων αριθμών Φιμπονάτσι πχ ότι  ή
ή  πρώτους αριθμούς, δεν είναι αποδεκτή;).
πρώτους αριθμούς, δεν είναι αποδεκτή;). που από το
που από το  ασκούν μια γοητεία πάνω μου αλλά και μου είναι χρήσιμες για ένα χόμπυ μου) και με τις παραπάνω παρατηρήσεις-διευκρινήσεις ακόμη περισσότερο.
ασκούν μια γοητεία πάνω μου αλλά και μου είναι χρήσιμες για ένα χόμπυ μου) και με τις παραπάνω παρατηρήσεις-διευκρινήσεις ακόμη περισσότερο.Για να κλείνει το θέμα ας δώσω ένα παράδειγμα που δείχνει ότι η παραπάνω τεχνική δεν οδηγεί πάντα στον ελάχιστο.ealexiou έγραψε: β). Ο μικρότερος πολλαπλάσιος του
είναι ο
και ο μικρότερος πολλαπλάσιος του
είναι, φυσικά, ο
, άρα ο ζητούμενος αριθμός είναι ο
και πράγματι στον πίνακα βλέπω: .
 .
. 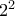 είναι ο
είναι ο  και ο μικρότερος που διαιρείται με τον
και ο μικρότερος που διαιρείται με τον  είναι ο
είναι ο  . Τότε ο παραπάνω συλλογισμός δίνει ως το μικρότερο πολλαπλάσιο του
. Τότε ο παραπάνω συλλογισμός δίνει ως το μικρότερο πολλαπλάσιο του  τον
τον  ( βλέπε εδώ)
( βλέπε εδώ) (βλέπε την ίδια παραπομπή) είναι μικρότερος.
(βλέπε την ίδια παραπομπή) είναι μικρότερος.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 12 επισκέπτες