 και το ύψος
και το ύψος  του συμμετρικού παραβολικού χωρίου του σχήματος , έχουν
του συμμετρικού παραβολικού χωρίου του σχήματος , έχουν σταθερό άθροισμα
 . Υπολογίστε το μέγιστο εμβαδόν του χωρίου . ( Στο σχήμα :
. Υπολογίστε το μέγιστο εμβαδόν του χωρίου . ( Στο σχήμα :  )
)Συντονιστής: Γιώργος Ρίζος
 και το ύψος
και το ύψος  του συμμετρικού παραβολικού χωρίου του σχήματος , έχουν
του συμμετρικού παραβολικού χωρίου του σχήματος , έχουν  . Υπολογίστε το μέγιστο εμβαδόν του χωρίου . ( Στο σχήμα :
. Υπολογίστε το μέγιστο εμβαδόν του χωρίου . ( Στο σχήμα :  )
)Έστω η παραβολή
 Στο σχήμα φαίνονται οι συντεταγμένες των
Στο σχήμα φαίνονται οι συντεταγμένες των  και είναι
και είναι
 Το εμβαδόν του παραβολικού χωρίου είναι:
Το εμβαδόν του παραβολικού χωρίου είναι:![\displaystyle E = 2\int_0^{\sqrt {\frac{b}{a}} } {\left( { - a{x^2} + b} \right)} dx = \left[ {bx - \frac{{a{x^3}}}{3}} \right]_0^{\sqrt {\frac{b}{a}} }\mathop \Leftrightarrow \limits^{(1)} \displaystyle E = 2\int_0^{\sqrt {\frac{b}{a}} } {\left( { - a{x^2} + b} \right)} dx = \left[ {bx - \frac{{a{x^3}}}{3}} \right]_0^{\sqrt {\frac{b}{a}} }\mathop \Leftrightarrow \limits^{(1)}](/forum/ext/geomar/texintegr/latexrender/pictures/b4c4513d21ed989e3ad54fea08007462.png)
 που παρουσιάζει μέγιστο
που παρουσιάζει μέγιστο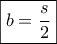 ίσο με
ίσο με 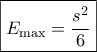
 , με μέγιστη
, με μέγιστη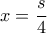 , την :
, την :  . Άρα :
. Άρα :  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 15 επισκέπτες