Σελίδα 1 από 1
Διχοτομήσεις
Δημοσιεύτηκε: Τετ Μαρ 21, 2018 2:54 pm
από KARKAR

- Διχοτομήσεις.png (13.12 KiB) Προβλήθηκε 590 φορές
Στο ορθογώνιο τρίγωνο

παρατηρήσαμε ότι η διχοτόμος

,
διχοτομεί το εμβαδόν του τριγώνου

, το οποίο σχηματίζει η διχοτόμος

με τις κάθετες πλευρές

. Υπολογίτε την :

.
Re: Διχοτομήσεις
Δημοσιεύτηκε: Τετ Μαρ 21, 2018 6:36 pm
από Doloros
Re: Διχοτομήσεις
Δημοσιεύτηκε: Τετ Μαρ 21, 2018 7:59 pm
από george visvikis
Ρίζα της εξίσωσης

Βρίσκω
![\displaystyle \tan B = \frac{1}{6}\left( {2 - \frac{{4\sqrt[3]{4}}}{{\sqrt[3]{{13 + 3\sqrt {33} }}}} + \sqrt[3]{{26 + 6\sqrt {33} }}} \right) \displaystyle \tan B = \frac{1}{6}\left( {2 - \frac{{4\sqrt[3]{4}}}{{\sqrt[3]{{13 + 3\sqrt {33} }}}} + \sqrt[3]{{26 + 6\sqrt {33} }}} \right)](/forum/ext/geomar/texintegr/latexrender/pictures/022a3a2392febe042037b2e748df0637.png)
Φαντάζομαι ότι είναι ίδιο με του Νίκου, αλλά δεν έχω το κουράγιο να το επαληθεύσω μετά από όλη τη διαδικασία.
Άρση απόκρυψης.
Re: Διχοτομήσεις
Δημοσιεύτηκε: Πέμ Μαρ 22, 2018 3:55 am
από Doloros

- Διχοτομήσεις.png (26.8 KiB) Προβλήθηκε 535 φορές
Φέρνω από το

παράλληλη στη διχοτόμο

. Επειδή

γιατί έχουν
κοινή βάση

και ίσα ύψη από τις δύο άλλες κορυφές θα είναι η
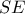
διάμεσος στο
τρίγωνο

. Έτσι θα έχω:

και

,

δηλαδή :

που λόγω των

έχω εξίσωση :

με μια πραγματική ρίζα :
![\boxed{x = \tan B = \sqrt[3]{{\frac{{\sqrt {33} }}{{36}} + \frac{{13}}{{108}}}} - \sqrt[3]{{\frac{{\sqrt {33} }}{{36}} - \frac{{13}}{{108}}}} + \frac{1}{3}} \boxed{x = \tan B = \sqrt[3]{{\frac{{\sqrt {33} }}{{36}} + \frac{{13}}{{108}}}} - \sqrt[3]{{\frac{{\sqrt {33} }}{{36}} - \frac{{13}}{{108}}}} + \frac{1}{3}}](/forum/ext/geomar/texintegr/latexrender/pictures/91a5028e9c1447ddc0753381443ae683.png)
Re: Διχοτομήσεις
Δημοσιεύτηκε: Πέμ Μαρ 22, 2018 8:50 am
από george visvikis
KARKAR έγραψε: ↑Τετ Μαρ 21, 2018 2:54 pm
Διχοτομήσεις.pngΣτο ορθογώνιο τρίγωνο

παρατηρήσαμε ότι η διχοτόμος

,
διχοτομεί το εμβαδόν του τριγώνου

, το οποίο σχηματίζει η διχοτόμος

με τις κάθετες πλευρές

. Υπολογίτε την :

.

- Διχοτομήσεις.png (12.86 KiB) Προβλήθηκε 519 φορές




Θέτω
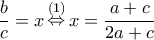
κι επειδή

θα είναι

οπότε καταλήγουμε στην

και
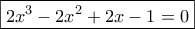
απ'όπου παίρνουμε τη
μοναδική ρίζα που έγραψα στην προηγούμενη ανάρτηση και που είναι προσεγγιστικά

 παρατηρήσαμε ότι η διχοτόμος
παρατηρήσαμε ότι η διχοτόμος  ,
, , το οποίο σχηματίζει η διχοτόμος
, το οποίο σχηματίζει η διχοτόμος 
 . Υπολογίτε την :
. Υπολογίτε την :  .
. παρατηρήσαμε ότι η διχοτόμος
παρατηρήσαμε ότι η διχοτόμος  ,
, , το οποίο σχηματίζει η διχοτόμος
, το οποίο σχηματίζει η διχοτόμος 
 . Υπολογίτε την :
. Υπολογίτε την :  .
.![\boxed{\varepsilon \varphi B = \sqrt[3]{{\frac{{\sqrt {33} }}{{36}} + \frac{{13}}{{108}}}} - \sqrt[3]{{\frac{{\sqrt {33} }}{{36}} - \frac{{13}}{{108}}}} + \frac{1}{3}} \boxed{\varepsilon \varphi B = \sqrt[3]{{\frac{{\sqrt {33} }}{{36}} + \frac{{13}}{{108}}}} - \sqrt[3]{{\frac{{\sqrt {33} }}{{36}} - \frac{{13}}{{108}}}} + \frac{1}{3}}](/forum/ext/geomar/texintegr/latexrender/pictures/46cf91d35ff76e5707b93d25d13745da.png)

![\displaystyle \tan B = \frac{1}{6}\left( {2 - \frac{{4\sqrt[3]{4}}}{{\sqrt[3]{{13 + 3\sqrt {33} }}}} + \sqrt[3]{{26 + 6\sqrt {33} }}} \right) \displaystyle \tan B = \frac{1}{6}\left( {2 - \frac{{4\sqrt[3]{4}}}{{\sqrt[3]{{13 + 3\sqrt {33} }}}} + \sqrt[3]{{26 + 6\sqrt {33} }}} \right)](/forum/ext/geomar/texintegr/latexrender/pictures/022a3a2392febe042037b2e748df0637.png)
 παράλληλη στη διχοτόμο
παράλληλη στη διχοτόμο  . Επειδή
. Επειδή  γιατί έχουν
γιατί έχουν  και ίσα ύψη από τις δύο άλλες κορυφές θα είναι η
και ίσα ύψη από τις δύο άλλες κορυφές θα είναι η 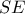 διάμεσος στο
διάμεσος στο  . Έτσι θα έχω:
. Έτσι θα έχω:  και
και  ,
,  δηλαδή :
δηλαδή : που λόγω των
που λόγω των  έχω εξίσωση :
έχω εξίσωση :  με μια πραγματική ρίζα :
με μια πραγματική ρίζα : ![\boxed{x = \tan B = \sqrt[3]{{\frac{{\sqrt {33} }}{{36}} + \frac{{13}}{{108}}}} - \sqrt[3]{{\frac{{\sqrt {33} }}{{36}} - \frac{{13}}{{108}}}} + \frac{1}{3}} \boxed{x = \tan B = \sqrt[3]{{\frac{{\sqrt {33} }}{{36}} + \frac{{13}}{{108}}}} - \sqrt[3]{{\frac{{\sqrt {33} }}{{36}} - \frac{{13}}{{108}}}} + \frac{1}{3}}](/forum/ext/geomar/texintegr/latexrender/pictures/91a5028e9c1447ddc0753381443ae683.png)




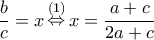 κι επειδή
κι επειδή  θα είναι
θα είναι  οπότε καταλήγουμε στην
οπότε καταλήγουμε στην και
και 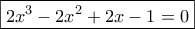 απ'όπου παίρνουμε τη
απ'όπου παίρνουμε τη 