
Άστοχο βέλος
Συντονιστής: Γιώργος Ρίζος
Άστοχο βέλος
Στο ημικύκλιο του σχήματος , ζητούμενο είναι το μήκος του "περίπου βέλους" 

Λέξεις Κλειδιά:
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15764
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Άστοχο βέλος
Το  απέχει από το μέσον της χορδής
απέχει από το μέσον της χορδής  απόσταση
απόσταση  . Αρα αν
. Αρα αν  η προβολή του
η προβολή του  στην διάμετρο
στην διάμετρο  , τότε το
, τότε το  απέχει από το κέντρο του
απέχει από το κέντρο του  κύκλου απόσταση (πάλι)
κύκλου απόσταση (πάλι)  . Από Πυθαγόρειο στο
. Από Πυθαγόρειο στο  είναι
είναι  . Αλλά αφού (πάλι από Πυθαγόρειο) η απόσταση
. Αλλά αφού (πάλι από Πυθαγόρειο) η απόσταση  της χορδής
της χορδής  από την διάμετρο
από την διάμετρο  είναι
είναι  , είναι
, είναι  .
.
 απέχει από το μέσον της χορδής
απέχει από το μέσον της χορδής  απόσταση
απόσταση  . Αρα αν
. Αρα αν  η προβολή του
η προβολή του  στην διάμετρο
στην διάμετρο  , τότε το
, τότε το  απέχει από το κέντρο του
απέχει από το κέντρο του  κύκλου απόσταση (πάλι)
κύκλου απόσταση (πάλι)  . Από Πυθαγόρειο στο
. Από Πυθαγόρειο στο  είναι
είναι  . Αλλά αφού (πάλι από Πυθαγόρειο) η απόσταση
. Αλλά αφού (πάλι από Πυθαγόρειο) η απόσταση  της χορδής
της χορδής  από την διάμετρο
από την διάμετρο  είναι
είναι  , είναι
, είναι  .
.- nickchalkida
- Δημοσιεύσεις: 312
- Εγγραφή: Τρί Ιουν 03, 2014 11:59 am
- Επικοινωνία:
Re: Άστοχο βέλος
Εναλλακτικά, επειδή  και
και 
για να βρούμε τα ,
,  επιλύουμε το σύστημα
επιλύουμε το σύστημα

που μας δίνει ,
, 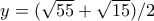 .
.
 και
και 
για να βρούμε τα
 ,
,  επιλύουμε το σύστημα
επιλύουμε το σύστημα
που μας δίνει
 ,
, 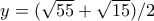 .
.- Συνημμένα
-
- velos.png (218.03 KiB) Προβλήθηκε 441 φορές
Μη είναι βασιλικήν ατραπόν επί την γεωμετρίαν.
- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5285
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: Άστοχο βέλος
Καλημέρα σε όλους. Επίσης, εναλλακτικά,
Έστω το μέσο του
το μέσο του  , οπότε το ημικύκλιο έχει εξίσωση
, οπότε το ημικύκλιο έχει εξίσωση  .
.
Οπότε, λόγω συμμετρίας, .
.
Aφού είναι σημεία του κύκλου, είναι .
.
Eπίσης, .
.
Η κάθετη τέμνει το ημικύκλιο στο
τέμνει το ημικύκλιο στο  , οπότε
, οπότε  .
.
Έστω
 το μέσο του
το μέσο του  , οπότε το ημικύκλιο έχει εξίσωση
, οπότε το ημικύκλιο έχει εξίσωση  .
.Οπότε, λόγω συμμετρίας,
 .
. Aφού είναι σημεία του κύκλου, είναι
 .
.Eπίσης,
 .
.Η κάθετη
 τέμνει το ημικύκλιο στο
τέμνει το ημικύκλιο στο  , οπότε
, οπότε  .
.Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 13 επισκέπτες
