 σημαίνει τον διψήφιο
σημαίνει τον διψήφιο  και όχι το γινόμενο
και όχι το γινόμενο 
Λοιπόν , βρείτε λύσεις για την παρακάτω - σωστή εν τέλει - απλοποίηση :

Συντονιστής: Γιώργος Ρίζος
 σημαίνει τον διψήφιο
σημαίνει τον διψήφιο  και όχι το γινόμενο
και όχι το γινόμενο 

Λάμπρος Κατσάπας έγραψε: ↑Σάβ Νοέμ 24, 2018 10:59 pmΤο κλασικό είναι το
Υπάρχουν και άλλα π.χ.(αυτά είναι όλα, το αφήνω ως άσκηση).
 και λοιπά της μορφής
και λοιπά της μορφής  και πολλά άλλα). Ακολουθεί μικρό απόσπασμα.
και πολλά άλλα). Ακολουθεί μικρό απόσπασμα. Δεν ψάχνουμε όλες τις περιπτώσεις αλλά αρκούν μερικές. Κατόπιν να βρεθούν παραδείγματα με
Δεν ψάχνουμε όλες τις περιπτώσεις αλλά αρκούν μερικές. Κατόπιν να βρεθούν παραδείγματα με  .
. πάλι έκανα λάθος με το
πάλι έκανα λάθος με το  . Στην θέση της ισότητας στα γινόμενα που μου ζήτησες, εγώ έψαξα την
. Στην θέση της ισότητας στα γινόμενα που μου ζήτησες, εγώ έψαξα την 
 και
και  και
και  και
και  και
και 
 και
και 
 και άλλα.
και άλλα. , με τα
, με τα  φυσικούς, θετικούς αριθμούς.
φυσικούς, θετικούς αριθμούς. , έχουμε
, έχουμε 
 , αφού είναι φυσικοί αριθμοί.
, αφού είναι φυσικοί αριθμοί. να είναι φυσικός άρα
να είναι φυσικός άρα  .
.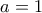 και
και  ο
ο  είναι φυσικός
είναι φυσικός  . Πράγματι,
. Πράγματι,  ... κ.ο.κ.
... κ.ο.κ. (1)
(1) και
και 
 αφού είναι παρανομαστής κλάσματος.
αφού είναι παρανομαστής κλάσματος. . Δηλαδή υπάρχει αριθμός
. Δηλαδή υπάρχει αριθμός 
 και
και 
 (2)
(2) (3)
(3) . Η σχέση (3) βρίσκουμε πως ισχύει για n=11,13,16,19 οπότε βρίσκομε τις αντίστοιχες τριάδες (a,b,c):(111),(2,6,5),(1,6,4),(1,9,5). Άρα έχουμε τους αριθμούς
. Η σχέση (3) βρίσκουμε πως ισχύει για n=11,13,16,19 οπότε βρίσκομε τις αντίστοιχες τριάδες (a,b,c):(111),(2,6,5),(1,6,4),(1,9,5). Άρα έχουμε τους αριθμούς  . Αντικαθιστώντας στην σχέση (1) παρατηρούμε πως ισχύουν.
. Αντικαθιστώντας στην σχέση (1) παρατηρούμε πως ισχύουν.Θεοδόση, για ξαναδές το αυτό. Για παράδειγμα, εφαρμόζεται στην ισότηταΘΕΟΔΟΣΙΟΣ ΦΩΤΙΑΔΗΣ έγραψε: ↑Κυρ Νοέμ 25, 2018 3:04 pm
Έχουμε:. Δηλαδή υπάρχει αριθμός
τέτοιος ώστεκαι
 ;
;Έχετε δίκιο κύριε Μιχάλη.Το αυθαίρετο βήμα στην λύση μου, ήταν να υποθέσω πως υπάρχει θετικός ακέραιοςMihalis_Lambrou έγραψε: ↑Κυρ Νοέμ 25, 2018 3:27 pmΘεοδόση, για ξαναδές το αυτό. Για παράδειγμα, εφαρμόζεται στην ισότηταΘΕΟΔΟΣΙΟΣ ΦΩΤΙΑΔΗΣ έγραψε: ↑Κυρ Νοέμ 25, 2018 3:04 pm
Έχουμε:. Δηλαδή υπάρχει αριθμός
τέτοιος ώστεκαι
;
 τέτοιος ώστε να διαιρεί ταυτόχρονα το
τέτοιος ώστε να διαιρεί ταυτόχρονα το  και το
και το  . Το ίδιο λάθος έκανα και με τα
. Το ίδιο λάθος έκανα και με τα  και
και  . Εκτός κι αν αποδείξω πως το
. Εκτός κι αν αποδείξω πως το  είναι πολλαπλάσιο των
είναι πολλαπλάσιο των  και
και 
Θεοδόσιε, πρώτα απ' όλα εύγε που ασχολείσαι με τα θέματα του φόρουμ. Εύχομαι να το απολαύσεις.ΘΕΟΔΟΣΙΟΣ ΦΩΤΙΑΔΗΣ έγραψε: ↑Κυρ Νοέμ 25, 2018 4:37 pmΕκτός κι αν αποδείξω πως τοείναι πολλαπλάσιο των
και


 δεν είναι σωστό, δηλαδή δεν προκύπτει από τις υποθέσεις. 'Ενας τρόπος να το δεις
δεν είναι σωστό, δηλαδή δεν προκύπτει από τις υποθέσεις. 'Ενας τρόπος να το δεις που έχεις ήδη προσδιορίσει. Σε αυτές το
που έχεις ήδη προσδιορίσει. Σε αυτές το  δεν
δεν .
. και
και  , συνεπώς η κλίση της είναι :
, συνεπώς η κλίση της είναι :  .
. , οπότε
, οπότε  . Άρα ο
. Άρα ο  θα διαιρεί το δεξί μέλος, αφού διαιρεί το αριστερό. Οπότε είτε
θα διαιρεί το δεξί μέλος, αφού διαιρεί το αριστερό. Οπότε είτε  ή
ή  , που σημαίνει ότι είτε
, που σημαίνει ότι είτε  (μη ξεχνάμε ότι
(μη ξεχνάμε ότι  αφού εμφανίζεται στον παρονομαστή) ή το
αφού εμφανίζεται στον παρονομαστή) ή το  είναι ένα από τα
είναι ένα από τα  . Με άλλα λόγια έχουμε κάποιο από τα
. Με άλλα λόγια έχουμε κάποιο από τα  .
.  μπορούμε εύκολα να βρούμε τις λύσεις, π.χ. με λίγες δοκιμές αλλά και με μικρά τεχνάσματα για να γλυτώσουμε κόπο. Π.χ. η
μπορούμε εύκολα να βρούμε τις λύσεις, π.χ. με λίγες δοκιμές αλλά και με μικρά τεχνάσματα για να γλυτώσουμε κόπο. Π.χ. η  δίνει
δίνει  , οπότε
, οπότε  συνεπώς
συνεπώς  ή
ή  ή
ή  , και λοιπά.
, και λοιπά.Σας ευχαριστώ, ήμουν αφηρημένος. Το οτιMihalis_Lambrou έγραψε: ↑Κυρ Νοέμ 25, 2018 5:38 pmΘεοδόσιε, πρώτα απ' όλα εύγε που ασχολείσαι με τα θέματα του φόρουμ. Εύχομαι να το απολαύσεις.ΘΕΟΔΟΣΙΟΣ ΦΩΤΙΑΔΗΣ έγραψε: ↑Κυρ Νοέμ 25, 2018 4:37 pmΕκτός κι αν αποδείξω πως τοείναι πολλαπλάσιο των
και


Το παραπάνω για τοδεν είναι σωστό, δηλαδή δεν προκύπτει από τις υποθέσεις. 'Ενας τρόπος να το δεις
είναι από τις λύσειςπου έχεις ήδη προσδιορίσει. Σε αυτές το
δεν
είναι πολλαπλάσιο του.
 δεν σημαίνει πως το
δεν σημαίνει πως το  είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  καθώς
καθώς  , Αυτό ισχύει μόνο όταν
, Αυτό ισχύει μόνο όταν  οπότε
οπότε  . Στην ουσία εγώ πήρα την ειδική περίπτωση στην οποία
. Στην ουσία εγώ πήρα την ειδική περίπτωση στην οποία  ενώ το σωστό είναι οτι
ενώ το σωστό είναι οτι  . Σωστή και όμορφη λύση είναι η δική σας.
. Σωστή και όμορφη λύση είναι η δική σας.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες