 , αν γνωρίζετε ότι :
, αν γνωρίζετε ότι :  και
και  . Απαραίτητη προϋπόθεση
. Απαραίτητη προϋπόθεσηγια να αποκτήσετε δικαίωμα απάντησης : Να δημοσιεύσετε δύο ( διαφορετικές ) λύσεις . Αμ πώς
Συντονιστής: Γιώργος Ρίζος
 , αν γνωρίζετε ότι :
, αν γνωρίζετε ότι :  και
και  . Απαραίτητη προϋπόθεση
. Απαραίτητη προϋπόθεση και τελειώνουμε.
β) Από Θεωρήματα διαμέσων:
και τελειώνουμε.
β) Από Θεωρήματα διαμέσων: 
 με την κάθετη από το
με την κάθετη από το  στη
στη  είναι το ζητούμενο σημείο
είναι το ζητούμενο σημείο 
 . Έστω
. Έστω  , οπότε
, οπότε  .
.
 .
. κι έχουμε προσδιορίσει τη θέση του
κι έχουμε προσδιορίσει τη θέση του  .
. .
.

 , οπότε
, οπότε  κι έχουμε προσδιορίσει τη θέση του
κι έχουμε προσδιορίσει τη θέση του  .
. . Κατόπιν την υπερβολή με εξίσωση
. Κατόπιν την υπερβολή με εξίσωση  και εντοπίζω το κοινό τους σημείο
και εντοπίζω το κοινό τους σημείο  στο θετικό τεταρτημόριο. Φέρω τις κάθετες
στο θετικό τεταρτημόριο. Φέρω τις κάθετες  και
και  στους άξονες
στους άξονες  αντίστοιχα. Κατασκευάζω τους κύκλους
αντίστοιχα. Κατασκευάζω τους κύκλους  και
και  που τέμνονται στο
που τέμνονται στο  . To
. To  είναι το τρίγωνο της υποθέσεως, άρα προσδιορίσαμε το
είναι το τρίγωνο της υποθέσεως, άρα προσδιορίσαμε το  .
. άρα η
άρα η 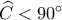 .Αν
.Αν 
 . Με Π. Θ. στα ορθογώνια τρίγωνα
. Με Π. Θ. στα ορθογώνια τρίγωνα 



 . Θα είναι
. Θα είναι  .
.  .
. και άρα :
και άρα : 
 και τέμνει την ευθεία
και τέμνει την ευθεία  στα
στα  με το
με το  ανάμεσα στα
ανάμεσα στα  και την
και την  (ακόμα στο
(ακόμα στο  .
.  . Έστω
. Έστω  , επειδή το τρίγωνο
, επειδή το τρίγωνο  είναι ισοσκελές θα είναι
είναι ισοσκελές θα είναι  .
. πέρα των
πέρα των 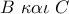 κατά τμήματα
κατά τμήματα  .
. και έχω από γενικευμένο Π. Θ. στα αμβλυγώνια τρίγωνα
και έχω από γενικευμένο Π. Θ. στα αμβλυγώνια τρίγωνα  :
:
 είναι ορθογώνιο στο
είναι ορθογώνιο στο  και άρα
και άρα  μετά με Π. Θ. έχω εύκολα τα ζητούμενα
μετά με Π. Θ. έχω εύκολα τα ζητούμενα
 και με βάση
και με βάση 
 ,
,  ,
,  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες