 - την εξίσωση :
- την εξίσωση : 
Συντονιστής: Γιώργος Ρίζος

![\boxed{x > \sqrt[3]{4}} \boxed{x > \sqrt[3]{4}}](/forum/ext/geomar/texintegr/latexrender/pictures/6b3bbbbfbab350da71ccd0f3ead6b3fe.png)

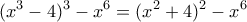

 απ' όπου
απ' όπου 
 ).
).
 . Αν λοιπόν δεν σκεφτόμασταν τόσο έξυπνα ,
. Αν λοιπόν δεν σκεφτόμασταν τόσο έξυπνα , ;
; είναι θετικό για
είναι θετικό για  . Δείξτε τουλάχιστον αυτό
. Δείξτε τουλάχιστον αυτό 

 . Οι δύο πρώτες έχουν διακρίνουσα αρνητική με μεταβλητές τις
. Οι δύο πρώτες έχουν διακρίνουσα αρνητική με μεταβλητές τις  αντίστοιχα και η τρίτη γιατί
αντίστοιχα και η τρίτη γιατί  . Αρα
. Αρα 

 και αντικαθιστώ:
και αντικαθιστώ: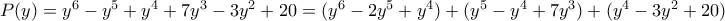
![=y^{4}(y-1)^{2}+y^{3}(y^{2}-y+7)+[(y^{2})^{2}-3y^{2}+20] =y^{4}(y-1)^{2}+y^{3}(y^{2}-y+7)+[(y^{2})^{2}-3y^{2}+20]](/forum/ext/geomar/texintegr/latexrender/pictures/6ab96564b27efb9b97c88fd01119679a.png)
 για τους δικούς του λόγους έκαστος επομένως
για τους δικούς του λόγους έκαστος επομένως 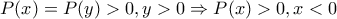

 την εξίσωση :
την εξίσωση : 

 είναι σαφέστατα πάνω από τον οριζόντιο άξονα.
είναι σαφέστατα πάνω από τον οριζόντιο άξονα. Η εξίσωση γράφεται
![\displaystyle{\sqrt[3]{x^2+4}=\sqrt{x^3-4}.} \displaystyle{\sqrt[3]{x^2+4}=\sqrt{x^3-4}.}](/forum/ext/geomar/texintegr/latexrender/pictures/1351a28f0184137d62573e9f99900a4a.png)
![\displaystyle{f(x)=\sqrt[3]{x^2+4}, x>0} \displaystyle{f(x)=\sqrt[3]{x^2+4}, x>0}](/forum/ext/geomar/texintegr/latexrender/pictures/af5ecb1671242377a11d687f41dabbc5.png)
 η οποία, κατά τα γνωστά, είναι ισοδύναμη με την
η οποία, κατά τα γνωστά, είναι ισοδύναμη με την 
 , η οποία έχει μοναδική ρίζα την
, η οποία έχει μοναδική ρίζα την 
 , η ρίζα (ας την πούμε
, η ρίζα (ας την πούμε  ) είναι θετική.
) είναι θετική.  οπότε η εξίσωση γράφεται
οπότε η εξίσωση γράφεται  .
.  είναι γνήσια φθίνουσα στο
είναι γνήσια φθίνουσα στο  και η
και η  γνήσια αύξουσα στο
γνήσια αύξουσα στο  , το οποίο περιέχει την ρίζα
, το οποίο περιέχει την ρίζα  . Επίσης είναι άμεσο ότι
. Επίσης είναι άμεσο ότι  για κάθε
για κάθε  .
.  θα είχαμε
θα είχαμε  , άτοπο (η
, άτοπο (η  είναι ρίζα).
είναι ρίζα). 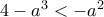 . Τελικά
. Τελικά  και άρα
και άρα 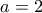 .
.Θέλουμε
 με
με  , οπότε
, οπότε  . Θέτουμε
. Θέτουμε  με
με  , οπότε
, οπότε 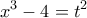 και
και  .
.  και άρα
και άρα  (χωρίς άλλη ρίζα διότι π.χ.
(χωρίς άλλη ρίζα διότι π.χ.  γνήσια αύξουσα στο
γνήσια αύξουσα στο  ).
).  σε οποιαδήποτε από τις δύο
σε οποιαδήποτε από τις δύο  δίνει
δίνει  , άρα
, άρα  .
.Φάνηκε ότι τα καλά ψάρια ήδη αλιεύτηκαν , να όμως που βρίσκουμε και άλλα λαβράκιαMihalis_Lambrou έγραψε: ↑Παρ Δεκ 14, 2018 11:10 pmΘέλουμεμε
, οπότε
. Θέτουμε
με
, οπότε
και
.
Προσθέτοντας κατά μέλη είναικαι άρα
(χωρίς άλλη ρίζα διότι π.χ.
γνήσια αύξουσα στο
).
Βάζονταςσε οποιαδήποτε από τις δύο
δίνει
, άρα
.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες