 του μαύρου κύκλου , θεωρούμε σημεία
του μαύρου κύκλου , θεωρούμε σημεία 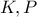 , ώστε :
, ώστε :  .
.Γράφουμε τον μπλε κύκλο
 , τον οποίο η κάθετη προς την
, τον οποίο η κάθετη προς την  στο
στο  τέμνει στο
τέμνει στο  .
.Α) Χαράξτε τον κόκκινο κύκλο
 , διερχόμενο από το
, διερχόμενο από το  και εφαπτόμενο του μαύρου .
και εφαπτόμενο του μαύρου .Β) Κάντε μια υπερπροσπάθεια να υπολογίσετε το μήκος της κοινής χορδή των εγχρώμων κύκλων .

 .
.
 που προφανώς διέρχεται από το
που προφανώς διέρχεται από το  και φέρνουμε την
και φέρνουμε την 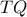 .
.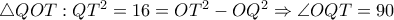 . Δηλ.
. Δηλ.  στο
στο  κατασκευάζεται αν βρούμε το κέντρο του
κατασκευάζεται αν βρούμε το κέντρο του 

 Εύκολα βρίσκω
Εύκολα βρίσκω  Το
Το  και
και  Άρα:
Άρα: 

 Λύνοντας το σύστημα των
Λύνοντας το σύστημα των  Από
Από 
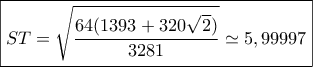
 . Αμ δε !
. Αμ δε ! )
)