Σελίδα 1 από 1
Αύξων λόγος
Δημοσιεύτηκε: Παρ Μαρ 15, 2019 1:37 pm
από KARKAR

- Αύξων λόγος.png (9.85 KiB) Προβλήθηκε 815 φορές

Σημείο

κινείται επί του ύψους

τριγώνου

, από το

προς το

.
Έστω ότι

. Δείξτε ότι ο λόγος

αυξάνει συνεχώς και εντοπίστε
εκείνη τη θέση του

, για την οποία ο λόγος αυτός γίνεται ίσος με

.
Re: Αύξων λόγος
Δημοσιεύτηκε: Παρ Μαρ 15, 2019 3:01 pm
από ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
KARKAR έγραψε: ↑Παρ Μαρ 15, 2019 1:37 pm
Αύξων λόγος.png

Σημείο

κινείται επί του ύψους

τριγώνου

, από το

προς το

.
Έστω ότι

. Δείξτε ότι ο λόγος

αυξάνει συνεχώς και εντοπίστε
εκείνη τη θέση του

, για την οποία ο λόγος αυτός γίνεται ίσος με

.
Το πρόβλημα "προσφέρεται" για αναλυτικοανάλυση


με

γνησίως αύξουσα στο

και επειδή η συνάρτηση

είναι γνησίως αύξουσα θα είναι και

γνησίως αύξουσα
Για να γίνει

Re: Αύξων λόγος
Δημοσιεύτηκε: Παρ Μαρ 15, 2019 3:54 pm
από STOPJOHN
KARKAR έγραψε: ↑Παρ Μαρ 15, 2019 1:37 pm
Αύξων λόγος.png

Σημείο

κινείται επί του ύψους

τριγώνου

, από το

προς το

.
Έστω ότι

. Δείξτε ότι ο λόγος

αυξάνει συνεχώς και εντοπίστε
εκείνη τη θέση του

, για την οποία ο λόγος αυτός γίνεται ίσος με

.
Εστω ότι

Τοτε


Γιάννης
Re: Αύξων λόγος
Δημοσιεύτηκε: Παρ Μαρ 15, 2019 4:40 pm
από george visvikis
Re: Αύξων λόγος
Δημοσιεύτηκε: Παρ Μαρ 15, 2019 8:02 pm
από KARKAR

- Αύξων λόγος.png (12.26 KiB) Προβλήθηκε 719 φορές
Γιώργο , πιθανότατα δεν κάνεις λάθος , σίγουρα όμως η λύση που προτείνεις είναι ελλιπής .
Διότι κατά την εκφώνηση αυξάνει το

. Το ότι αυξάνει ταυτόχρονα και το

θέλει απόδειξη .
Φαίνεται πάντως ότι πράγματι έτσι συμβαίνει .
Re: Αύξων λόγος
Δημοσιεύτηκε: Παρ Μαρ 15, 2019 8:16 pm
από george visvikis
KARKAR έγραψε: ↑Παρ Μαρ 15, 2019 8:02 pm
Αύξων λόγος.png Γιώργο , πιθανότατα δεν κάνεις λάθος , σίγουρα όμως η λύση που προτείνεις είναι ελλιπής .
Διότι κατά την εκφώνηση αυξάνει το

. Το ότι αυξάνει ταυτόχρονα και το

θέλει απόδειξη .
Φαίνεται πάντως ότι πράγματι έτσι συμβαίνει .
Σ' ευχαριστώ Θανάση για την άμεση απάντηση. Κάτι δεν μου πήγαινε καλά... δικαιολογημένα, απ' ότι φαίνεται.
Re: Αύξων λόγος
Δημοσιεύτηκε: Κυρ Μαρ 17, 2019 8:44 am
από Mihalis_Lambrou
KARKAR έγραψε: ↑Παρ Μαρ 15, 2019 1:37 pm
Σημείο

κινείται επί του ύψους

τριγώνου

, από το

προς το

.
Έστω ότι

. Δείξτε ότι ο λόγος

αυξάνει συνεχώς και εντοπίστε
εκείνη τη θέση του

, για την οποία ο λόγος αυτός γίνεται ίσος με

.
Ας το δούμε και Τριγωνομετρικά: Αν

έχουμε αμέσως ότι

. Το τετράγωνο του δοθέντα λόγου είναι

Είναι τώρα άμεσο ότι καθώς αυξάνει το

, αυξάνει και το δεξί μέλος. Τα υπόλοιπα απλά.
 Σημείο
Σημείο  κινείται επί του ύψους
κινείται επί του ύψους  τριγώνου
τριγώνου  , από το
, από το  προς το
προς το  .
. . Δείξτε ότι ο λόγος
. Δείξτε ότι ο λόγος  αυξάνει συνεχώς και εντοπίστε
αυξάνει συνεχώς και εντοπίστε , για την οποία ο λόγος αυτός γίνεται ίσος με
, για την οποία ο λόγος αυτός γίνεται ίσος με  .
. με
με  γνησίως αύξουσα στο
γνησίως αύξουσα στο  και επειδή η συνάρτηση
και επειδή η συνάρτηση  είναι γνησίως αύξουσα θα είναι και
είναι γνησίως αύξουσα θα είναι και  γνησίως αύξουσα
γνησίως αύξουσα



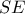 της
της  και έστω
και έστω 


 . Το ότι αυξάνει ταυτόχρονα και το
. Το ότι αυξάνει ταυτόχρονα και το  θέλει απόδειξη .
θέλει απόδειξη . έχουμε αμέσως ότι
έχουμε αμέσως ότι  . Το τετράγωνο του δοθέντα λόγου είναι
. Το τετράγωνο του δοθέντα λόγου είναι 
 , αυξάνει και το δεξί μέλος. Τα υπόλοιπα απλά.
, αυξάνει και το δεξί μέλος. Τα υπόλοιπα απλά.