minageus έγραψε: ↑Τρί Ιουν 04, 2019 6:44 pm
Αναφέρεστε στην σταθερά Euler-Masceroni;
Ναι.
minageus έγραψε: ↑Τρί Ιουν 04, 2019 6:44 pm
Θα μπορούσατε να παραθέσετε κάποια ενδεικτική λύση;
Χαριτολογώντας ισχυρίστηκα ότι μπορούμε να προσεγγίσουμε το

φυσώντας κεράκια.
Είναι γνωστό ότι

ή καλύτερα

από την οποία παίρνουμε

Αν λοιπόν έχουμε ''πολλά'' κεράκια και θέλουμε να εκτιμήσουμε π.χ. το

μπορούμε να φυσάμε

άδες και κάθε φορά να μετράμε πόσες φορές χρειάστηκε να φυσήξουμε. Μετά από ''πολλές'' κατεστραμμένες

άδες, παίρνοντας τον μέσο όρο των απαιτούμενων φυσιμάτων, αναμένουμε από τον Νόμο των Μεγάλων
Αριθμών να βρούμε αριθμό ''κοντά'' στην μέση τιμή που είναι

Συνυπολογίζοντας
τώρα το τυχαίο σφάλμα που προκύπτει από την προσέγγιση της μέσης τιμής από τον μέσο όρο και χρησιμοποιώντας την

εκτιμούμε το
 Υ.Γ.
Υ.Γ. Εντάξει δεν είναι και η καλύτερη προσέγγιση που μπορούμε να κάνουμε αφού μπορούμε να κάνουμε εκτίμηση
κατευθείαν από την

αλλά σαν ιδέα καλή ακούγεται νομίζω.
Θυμίζει την προσέγγιση του

πετώντας βελάκια σε στόχο ή την προσέγγιση του

από τον ελάχιστο
αριθμό ομοιόμορφων τ.μ. που πρέπει να αθροίσουμε μέχρι να ξεπεράσουμε το

Ούτως ή άλλως πολλά προβλήματα στα οποία η αναλυτική ή αριθμητική λύση είναι ανέφικτη η προσέγγιση μέσω
στοχαστικών πειραμάτων μας δίνει τη λύση.
 και γιορτάζεις τα γενέθλιά σου με μια τούρτα που έχει πάνω της
και γιορτάζεις τα γενέθλιά σου με μια τούρτα που έχει πάνω της  κεριά.
κεριά.  και του αριθμού των κεριών που παραμένουν αναμμένα. Πόσες φορές, κατά μέσο όρο,
και του αριθμού των κεριών που παραμένουν αναμμένα. Πόσες φορές, κατά μέσο όρο, 
 για τις αναμενόμενες φορές που χρειάζεται να φυσήξει, παίρνουμε την αναδρομική σχέση
για τις αναμενόμενες φορές που χρειάζεται να φυσήξει, παίρνουμε την αναδρομική σχέση  με την αρχική συνθήκη
με την αρχική συνθήκη  . Επαγωγικά μπορεί να αποδειχθεί ότι
. Επαγωγικά μπορεί να αποδειχθεί ότι  .
. (τυχαία μεταβλητή) ο χρόνος (αριθμός φυσημάτων) που υπολείπεται για να τερματιστεί η διαδικασία
(τυχαία μεταβλητή) ο χρόνος (αριθμός φυσημάτων) που υπολείπεται για να τερματιστεί η διαδικασία  κεράκια (
κεράκια ( ). Εμείς αναζητούμε την αναμενόμενη τιμή
). Εμείς αναζητούμε την αναμενόμενη τιμή  .
.

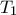 , με πιθανότητα
, με πιθανότητα  κεριά
κεριά  κ.ο.κ. .
κ.ο.κ. . 

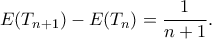 Αθροίζοντας τις τελευταίες για
Αθροίζοντας τις τελευταίες για  παίρνουμε
παίρνουμε  και συνεπώς
και συνεπώς  .
. βρίσκουμε
βρίσκουμε 
 λαμβάνοντας υπόψη και τη σταθερά
λαμβάνοντας υπόψη και τη σταθερά 



 μπορούμε να φυσάμε
μπορούμε να φυσάμε  Συνυπολογίζοντας
Συνυπολογίζοντας 

 πετώντας βελάκια σε στόχο ή την προσέγγιση του
πετώντας βελάκια σε στόχο ή την προσέγγιση του  από τον ελάχιστο
από τον ελάχιστο 