Σελίδα 1 από 1
Χαρταετός - μαυραετός
Δημοσιεύτηκε: Δευ Νοέμ 25, 2019 1:22 pm
από KARKAR

- Χαρταετός - μαυραετός.png (11.87 KiB) Προβλήθηκε 411 φορές
Στο ορθογώνιο

, εγγράψαμε τον χαρταετό

. Ορθογώνιο και χαρταετός έχουν
πλευρές με ακέραια μήκη . Φτιάξε ένα τέτοιο σχήμα , με όσο γίνεται μικρότερα μήκη πλευρών.
Ιδιαιτέρως ενδιαφέρομαι για την περίπτωση που :

.
Re: Χαρταετός - μαυραετός
Δημοσιεύτηκε: Δευ Νοέμ 25, 2019 5:16 pm
από george visvikis
KARKAR έγραψε: ↑Δευ Νοέμ 25, 2019 1:22 pm
Χαρταετός - μαυραετός.pngΣτο ορθογώνιο

, εγγράψαμε τον χαρταετό

. Ορθογώνιο και χαρταετός έχουν
πλευρές με ακέραια μήκη . Φτιάξε ένα τέτοιο σχήμα , με όσο γίνεται μικρότερα μήκη πλευρών.
Ιδιαιτέρως ενδιαφέρομαι για την περίπτωση που :

.

- Χαρταετός-μαυραετός.png (12.72 KiB) Προβλήθηκε 389 φορές
Μάλλον θα θέλετε και αιτιολόγηση

(εκτός κι αν αμφισβητείται το σχήμα μου).
Re: Χαρταετός - μαυραετός
Δημοσιεύτηκε: Δευ Νοέμ 25, 2019 5:46 pm
από george visvikis
Re: Χαρταετός - μαυραετός
Δημοσιεύτηκε: Τρί Νοέμ 26, 2019 4:15 am
από Doloros
Έστω:


. Π. Θ. στο
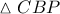
:

.
Άρα

, οπότε:

Κατασκευή :
Έστω ορθογώνιο τρίγωνο

με πλευρές ακεραίους ( Πυθαγόρεια τριάδα)

πρέπει όμως να υπάρχει θετικός ακέραιος

και να ισχύει :

και

Παραδείγματα :

- μαυραετός χαρταετός.png (8.28 KiB) Προβλήθηκε 353 φορές
α)

β) Η μικρότερη δυάδα

έτσι όπως πιο πάνω:

και

. Εδώ έχουμε και το ζητούμενο λόγο .
γ)


, άρα

 , εγγράψαμε τον χαρταετό
, εγγράψαμε τον χαρταετό  . Ορθογώνιο και χαρταετός έχουν
. Ορθογώνιο και χαρταετός έχουν .
. , εγγράψαμε τον χαρταετό
, εγγράψαμε τον χαρταετό  . Ορθογώνιο και χαρταετός έχουν
. Ορθογώνιο και χαρταετός έχουν .
.




 και αντικαθιστώντας στην
και αντικαθιστώντας στην 




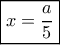

 . Π. Θ. στο
. Π. Θ. στο 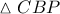 :
:  .
.  , οπότε:
, οπότε: 
 με πλευρές ακεραίους ( Πυθαγόρεια τριάδα)
με πλευρές ακεραίους ( Πυθαγόρεια τριάδα)  πρέπει όμως να υπάρχει θετικός ακέραιος
πρέπει όμως να υπάρχει θετικός ακέραιος  και να ισχύει :
και να ισχύει : και
και 

 έτσι όπως πιο πάνω:
έτσι όπως πιο πάνω: και
και  . Εδώ έχουμε και το ζητούμενο λόγο .
. Εδώ έχουμε και το ζητούμενο λόγο .
 , άρα
, άρα 