1. Να δειχθεί η ισότητα
 .
.2. Σε ένα κύκλο
 να εγγραφεί κανονικό τρίγωνο (ισόπλευρο) και να υπολογιστεί η πλευρά και το απόστημά του από την ακτίνα του κύκλου.
να εγγραφεί κανονικό τρίγωνο (ισόπλευρο) και να υπολογιστεί η πλευρά και το απόστημά του από την ακτίνα του κύκλου.3.α. Αν
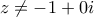 και
και  , δείξτε ότι :
, δείξτε ότι :i) Όταν
 τότε ο αριθμός
τότε ο αριθμός  είναι καθαρός φανταστικός.
είναι καθαρός φανταστικός.ii) Όταν ο αριθμός
 είναι καθαρός φανταστικός τότε
είναι καθαρός φανταστικός τότε  .
.β. Να βρείτε το μέτρο και το όρισμα του μιγαδικού
 .
.4.α. Έστω
 ένας διανυσματικός χώρος πάνω στο σώμα
ένας διανυσματικός χώρος πάνω στο σώμα  . Αν
. Αν  και
και  είναι διανυσματικοί υπόχωροι του
είναι διανυσματικοί υπόχωροι του  ,
, να δείξετε ότι το σύνολο
 δεν είναι το κενό και μάλιστα είναι υπόχωρος του
δεν είναι το κενό και μάλιστα είναι υπόχωρος του  .
.β. Αν
 είναι τρία γραμμικώς ανεξάρτητα στοιχεία ενός γραμμικού διανυσματικού χώρου,
είναι τρία γραμμικώς ανεξάρτητα στοιχεία ενός γραμμικού διανυσματικού χώρου, να δείξετε ότι και τα στοιχεία
 είναι επίσης γραμμικώς ανεξάρτητα .
είναι επίσης γραμμικώς ανεξάρτητα .

 και
και  .Τότε θα ισχύει,
.Τότε θα ισχύει, , γεγονός που αποδεικνύει ότι το σύνολο
, γεγονός που αποδεικνύει ότι το σύνολο είναι διανυσματικός υπόχωρος του
είναι διανυσματικός υπόχωρος του  τέτοια, ώστε
τέτοια, ώστε  .Συνεπώς,
.Συνεπώς,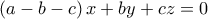 .
.
 είναι γραμμικώς ανεξάρτητα.
είναι γραμμικώς ανεξάρτητα.






![z = - \sigma \upsilon \nu \theta + i\eta \mu \theta \Rightarrow z = \left| z \right|\left[ {\sigma \upsilon \nu \left( {\pi - \theta } \right) + i\eta \mu \left( {\pi - \theta } \right)} \right] z = - \sigma \upsilon \nu \theta + i\eta \mu \theta \Rightarrow z = \left| z \right|\left[ {\sigma \upsilon \nu \left( {\pi - \theta } \right) + i\eta \mu \left( {\pi - \theta } \right)} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/a8dad5644415cf12fd8e99bb6e5b680e.png)
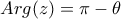
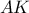 ,
, 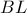 διάμεσοι ισχύει ότι:
διάμεσοι ισχύει ότι: 
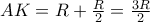
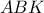 έχω ότι ημ60=
έχω ότι ημ60=
 και το απόστημα ίσο με
και το απόστημα ίσο με 