Συνήθως ήταν ξεχωριστά τα θέματα Άλγεβρας , Γεωμετρίας και Τριγωνομετρίας.
Τα αρχικά σημαίνουν ΠΟΛΥΤΕΧΝ(ΙΚΟΣ) - ΦΥΣΙΚΟΜΑΘ(ΗΜΑΤΙΚΟΣ) -ΓΕΩ(ΠΟΝΟ)ΔΑΣ(ΟΛΟΓΙΚΟΣ) ΚΥΚΛΟΣ .
Άλλοτε οι παραπάνω κύκλοι είχαν διαφορετικά θέματα, άλλοτε είχαν κοινά θέματα.
Ταξινομημένα συγκεντρώνονται και τα παραπάνω θέματα σαν προτείνονται στο Ευρετήριο Θεμάτων Πανελλαδικών Εξετάσεων.
1. Αν
 , όπου
, όπου  είναι δοσμένοι μιγαδικοί αριθμοί,
είναι δοσμένοι μιγαδικοί αριθμοί, να δείξετε ότι
 για κάθε πραγματικό αριθμό
για κάθε πραγματικό αριθμό  . Πότε μπορεί να ισχύει η ισότητα;
. Πότε μπορεί να ισχύει η ισότητα;2. α) Τι καλείται συνδυασμός των
 πραγμάτων ανά
πραγμάτων ανά  ;
;β) Να αποδείξετε τον τύπο που δίνει το πλήθος των συνδυασμών των
 πραγμάτων ανά
πραγμάτων ανά  . Υποτίθεται ότι
. Υποτίθεται ότι 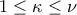 .
.3. α) Πότε μια συνάρτηση
 λέγεται συνεχής σε ένα σημείο
λέγεται συνεχής σε ένα σημείο  του πεδίου ορισμού της;
του πεδίου ορισμού της; Πότε μια συνάρτηση
 λέγεται συνεχής σε ένα διάστημα;
λέγεται συνεχής σε ένα διάστημα;β) Να εξετάσετε αν η συνάρτηση
 που δίνεται από το τύπο
που δίνεται από το τύπο 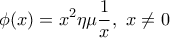
και
 είναι συνεχής στο σύνολο των πραγματικών αριθμών.
είναι συνεχής στο σύνολο των πραγματικών αριθμών.4. Δίνεται ένα πολυώνυμο με πραγματικούς συντελεστές
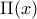 βαθμού
βαθμού 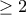 .
.α) Να δείξετε ότι αν ο πραγματικός αριθμός
 είναι πολλαπλή ρίζα του
είναι πολλαπλή ρίζα του 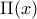 τότε ο
τότε ο  είναι ρίζα της παραγώγου του
είναι ρίζα της παραγώγου του 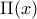 .
.β) Με τη βοήθεια της προηγούμενης ιδιότητας να προσδιορίσετε τους πραγματικούς αριθμούς
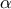 και
και  ώστε
ώστε το πολυώνυμο
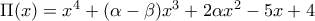 να έχει πολλαπλή ρίζα τον αριθμό
να έχει πολλαπλή ρίζα τον αριθμό  .
.edit
Απλούστευση ονομασίας
μετονομασία


 πραγμάτων ανά
πραγμάτων ανά  με
με 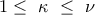 , (συμβολικά
, (συμβολικά  ) ονομάζουμε κάθε υποσύνολο του
) ονομάζουμε κάθε υποσύνολο του  ,το οποίο περιέχει
,το οποίο περιέχει 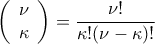
 το πλήθος των συνδυασμών των
το πλήθος των συνδυασμών των  στοιχείων , που είναι
στοιχείων , που είναι  , θα πάρουμε
, θα πάρουμε 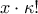 διατάξεις των
διατάξεις των  )
)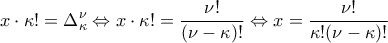
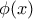 είναι γινόμενο μηδενικής επί φραγμένης άρα το όριο στο μηδέν θα ισούται με μηδέν, άρα έχουμε:
είναι γινόμενο μηδενικής επί φραγμένης άρα το όριο στο μηδέν θα ισούται με μηδέν, άρα έχουμε: ,
,