ΕΜΠ 1962 ΓΕΩΜΕΤΡΙΑ ΑΡΧΙΤΕΚΤΟΝΕΣ

parmenides51 · #1

Εξεταστής: Α. Σφήκας

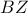1. Σε τρίγωνο $\displaystyle{AB\Gamma}$ και πάνω στις πλευρές $\displaystyle{AB}$ και $\displaystyle{A\Gamma}$ κατασκευάζουμε εξωτερικά του τριγώνου τα τετράγωνα $\displaystyle{AB\Delta {\color{red}E}}$ και $\displaystyle{A\Gamma ZH}$ . Φέρνουμε τις $\displaystyle{ EH,\Delta\Gamma}$ και $\displaystyle{BZ}$ . Ζητείται να αποδειχθεί οτι
α) Η από το $\displaystyle{A}$ κάθετη στην $\displaystyle{EH}$ είναι διάμεσος του τριγώνου $\displaystyle{AB\Gamma}$
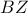β) Το σημείο τομής των καθέτων από τα $\displaystyle{B}$ και $\displaystyle{\Gamma}$ προς τις $\displaystyle{\Gamma\Delta}$ και $\displaystyle{BZ}$ αντίστοιχα βρίσκεται πάνω στην κάθετο $\displaystyle{AP}$ που άγεται από το $\displaystyle{A}$ προς την $\displaystyle{B\Gamma}$ .
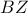γ) Οι ευθείες $\displaystyle{\Delta\Gamma}$ και $\displaystyle{BZ}$ τέμνονται πάνω στην $\displaystyle{AP}$ .

2. Κύκλος κέντρου $\displaystyle{O}$ κι ακτίνας $\displaystyle{R}$ , εφάπτεται στο μέσο $\displaystyle{M}$ δεδομένου τμήματος $\displaystyle{AB}$ . Έστω $\displaystyle{\Gamma\Delta}$ η εφαπτομένη του κύκλου από κάποιο σημείο $\displaystyle{\Gamma}$ . Ζητείται ο γεωμετρικός τόπος των σημείων $\displaystyle{ \Gamma}$ , για τα οποία θα ισχύει η σχέση $\displaystyle{(\Gamma A)^2+(\Gamma B)^2=4(\Gamma \Delta)^2}$ .

3. Να δείξετε οτι αν σε τετράεδρο $\displaystyle{KAB\Gamma}$ είναι $\displaystyle{(KA)^2-(B\Gamma)^2=(KB)^2-(\Gamma A)^2=(K\Gamma)^2-(AB)^2}$ τότε η κορυφή $\displaystyle{K}$ του τετραέδρου προβάλλεται πάνω στην απέναντι έδρα $\displaystyle{AB\Gamma}$ σε σημείο, το οποίο είναι συμμετρικό του ορθοκέντρου ως προς το κέντρο του περιγεγραμμένου κύκλου κι αντιστρόφως.

4. Έστω $\displaystyle{AB\Gamma}$ ισοσκελές ορθογώνιο τρίγωνο με υποτείνουσα $\displaystyle{B\Gamma=2\alpha}$ . Από σημείο $\displaystyle{M}$ του χώρου φέρνουμε τις καθέτους $\displaystyle{MA' }$ πάνω στην πλευρά του τριγώνου $\displaystyle{B\Gamma, MB'}$ πάνω στην $\displaystyle{ A\Gamma }$ και $\displaystyle{M\Gamma'}$ πάνω στην $\displaystyle{AB}$ . Ζητείται να βρεθεί ο γεωμετρικός τόπος των σημείων $\displaystyle{M }$ του χώρου, για τα οποία είναι $\displaystyle{\frac{MA'}{2\alpha}=\frac{MB'}{\alpha\sqrt2}=\frac{M\Gamma''}{\alpha\sqrt2}}$

Σημείωση: το 1ο θέμα έπεσε και στις εξετάσεις των Αλλοδαπών ΕΜΠ (εδώ)

Υ.Γ. Σύμφωνα με το Ετήσιο Δελτίο του Πάλλα το θέμα 4 ήταν εκτός της τότε εξεταστέας ύλης
(στις μια από τις δυο περιπτώσεις της λύσης βγαίνει παραβολή, η οποία ήταν τότε εκτός ύλης)
Ήταν ένα από τα 6 θέματα των εισαγωγικών εξετάσεων του ΕΜΠ το 1962 για τα οποία κατέθεσε μήνυση ο Αριστείδης Πάλλας
στο Συμβούλιο της Επικρατείας και ζητούσε την ακύρωση των τότε εξετάσεων. Το μέρος του πήρε η ΕΜΕ τότε.
Περισσότερα προσεχώς αφού ανέβουν και τα 6 θέματα.
Προτροπή: Αναζητήστε την ''Μαύρη Βίβλο των Εισαγωγικών Εξετάσεων του Εθνικού Μετσόβιου Πολυτεχνείου κατά Σεπτέμβριον 1962''
του Αριστείδου Φ. Πάλλα (περιέχει το ιστορικό των ακυρωθέντων θεμάτων και δημοσιεύματα εφημερίδων της εποχής)
Για να το διαβάσετε έχει 4 αντίτυπα η μη δανειστική Μπενάκειος Βιβλιοθήκη
η οποία στεγάζεται προς το παρόν στο Πρώην Δημόσιο Καπνεργοστάσιο (Λένορμαν 218, Αθήνα)
Τους κωδικούς τους βλέπετε με την αναζήτηση ''Η μαύρη βίβλος των εισαγωγικών εξετάσεων'' εδώ
Ώρες λειτουργίας: Δευτέρα και Τετάρτη 9:00-18:00, Τρίτη, Πέμπτη και Παρασκευή 9:00-15:00, Σάββατο 9:00-14:00
Επικοινωνία: (Αναγνωστήριο) 210 510 2059
Πληροφορίες εδώ

edit's
διόρθωση τυπογραφικού στο 1ο, ευχαριστώ τον Γιώργο (Βισβίκη) που το πρόσεξε
προσθήκη σημείωσης

#2

parmenides51 έγραψε:Εξεταστής: Α. Σφήκας

1. Σε τρίγωνο $\displaystyle{AB\Gamma}$ και πάνω στις πλευρές $\displaystyle{AB}$ και $\displaystyle{A\Gamma}$ κατασκευάζουμε εξωτερικά του τριγώνου τα τετράγωνα $\displaystyle{AB\Delta {\color{red}E}}$ και $\displaystyle{A\Gamma ZH}$ . Φέρνουμε τις $\displaystyle{ EH,\Delta\Gamma}$ και $\displaystyle{BZ}$ . Ζητείται να αποδειχθεί οτι
α) Η από το $\displaystyle{A}$ κάθετη στην $\displaystyle{EH}$ είναι διάμεσος του τριγώνου $\displaystyle{AB\Gamma}$
β) Το σημείο τομής των καθέτων από τα $\displaystyle{B}$ και $\displaystyle{\Gamma}$ προς τις $\displaystyle{\Gamma\Delta}$ και $\displaystyle{BZ}$ αντίστοιχα βρίσκεται πάνω στην κάθετο $\displaystyle{AP}$ που άγεται από το $\displaystyle{A}$ προς την $\displaystyle{B\Gamma}$ .
γ) Οι ευθείες $\displaystyle{\Delta\Gamma}$ και $\displaystyle{BZ}$ τέμνονται πάνω στην $\displaystyle{AP}$ .

Καλημέρα.

α) Έστω

η διάμεσος του τριγώνου $\displaystyle{{\rm A}{\rm B}\Gamma }$ και

το κοινό σημείο των

και

. Θα δείξω ότι $\displaystyle{{\rm A}{\rm K} \bot {\rm E}{\rm H}}$ .

: ΕΜΠ 1962.png (24.78 KiB) Προβλήθηκε 1622 φορές

Προεκτείνω την

κατά τμήμα MN=AM

. Το τετράπλευρο $\displaystyle{{\rm A}\Gamma {\rm N}{\rm B}}$ είναι παραλληλόγραμμο (οι διαγώνιες του διχοτομούνται). Άρα, $\displaystyle{\Gamma {\rm N} = {\rm A}{\rm B} = {\rm A}{\rm E},{\rm A}\Gamma = {\rm A}{\rm H}}$ .
Εξάλλου, $\displaystyle{{\rm A}\widehat \Gamma {\rm N} + \widehat {\rm A} = {180^0}}$ ( $\displaystyle{\widehat {\rm A}}$ , η γωνία του τριγώνου $\displaystyle{{\rm A}{\rm B}\Gamma }$ ) και $\displaystyle{{\rm E}\widehat {\rm A}{\rm H} + \widehat {\rm A} = {180^0}}$ . Οπότε $\displaystyle{{\rm E}\widehat {\rm A}{\rm H} = {\rm A}\widehat \Gamma {\rm N}}$ . Δηλαδή τα τρίγωνα $\displaystyle{{\rm E}{\rm A}{\rm H},{\rm A}\Gamma {\rm N}}$ είναι ίσα (Π - Γ - Π). Από την ισότητα των τριγώνων προκύπτει ότι $\displaystyle{{\widehat {\rm A}_1} = {\widehat {\rm H}_1}}$ . Αλλά $\displaystyle{{\widehat {\rm A}_1} + {\widehat {\rm A}_2} = {90^0}}$ , οπότε $\displaystyle{{\widehat {\rm H}_1} + {\widehat {\rm A}_2} = {90^0} \Leftrightarrow {\rm A}{\rm K} \bot {\rm E}{\rm H}}$ .

: ΕΜΠ 1962.2png.png (21.92 KiB) Προβλήθηκε 1622 φορές

β) Έστω ότι η $\displaystyle{\Gamma {\rm T} \bot {\rm B}{\rm Z}}$ τέμνει την ευθεία του ύψους

του τριγώνου $\displaystyle{{\rm A}{\rm B}\Gamma }$ στο σημείο $\displaystyle{\Lambda }$ .
Τα τρίγωνα $\displaystyle{{\rm B}\Gamma {\rm Z},\Lambda {\rm A}\Gamma }$ είναι ίσα, γιατί έχουν:
$\displaystyle{\Gamma {\rm Z} = {\rm A}\Gamma }$ και $\displaystyle{{\widehat {\rm Z}_1} = {\widehat \Gamma _1}}$ (οξείες γωνίες με πλευρές κάθετες), $\displaystyle{{\rm B}\widehat \Gamma {\rm Z},\Lambda \widehat {\rm A}\Gamma }$ (αμβλείες γωνίες με πλευρές κάθετες). Άρα, $\displaystyle{{\rm B}\Gamma = {\rm A}\Lambda }$ (1)

Αν η $\displaystyle{{\rm B}\Sigma \bot \Gamma \Delta }$ τέμνει την ευθεία του ύψους

του τριγώνου $\displaystyle{{\rm A}{\rm B}\Gamma }$ στο σημείο $\displaystyle{\Lambda_1 }$ , τότε ομοίως αποδεικνύεται ότι τα τρίγωνα $\displaystyle{{\rm B}\Gamma \Delta ,{\rm A}{\Lambda _1}{\rm B}}$ είναι ίσα, οπότε $\displaystyle{{\rm B}\Gamma = {\rm A}{\Lambda _1}}$ (2).
Από (1), (2), τα σημεία $\displaystyle{\Lambda ,{\Lambda _1}}$ συμπίπτουν. Άρα οι $\displaystyle{{\rm B}\Sigma ,\Gamma {\rm T}}$ τέμνονται πάνω στην ευθεία του ύψους

.

γ) Στο τρίγωνο $\displaystyle{\Lambda {\rm B}\Gamma }$ , τα τμήματα $\displaystyle{\Lambda {\rm P},{\rm B}{\rm T},\Gamma \Sigma }$ είναι ύψη, άρα διέρχονται από το ίδιο σημείο

που είναι και το ορθόκεντρο. Επομένως οι ευθείες $\displaystyle{{\rm B}{\rm Z},\Gamma \Delta }$ τέμνονται πάνω στο ύψος του τριγώνου $\displaystyle{{\rm A}{\rm B}\Gamma }$ .

Σημείωση: Τα τρία αυτά ερωτήματα είναι από το θεώρημα του Vecten.

ΕΜΠ 1962 ΓΕΩΜΕΤΡΙΑ ΑΡΧΙΤΕΚΤΟΝΕΣ

ΕΜΠ 1962 ΓΕΩΜΕΤΡΙΑ ΑΡΧΙΤΕΚΤΟΝΕΣ

Re: ΕΜΠ 1962 ΓΕΩΜΕΤΡΙΑ ΑΡΧΙΤΕΚΤΟΝΕΣ

Μέλη σε σύνδεση