Μια Χριστουγεννιάτικη.
α) Μια ημέρα άρχισε να πέφτει πυκνό χιόνι με σταθερό ρυθμό. Ένα εκχιονιστικό όχημα ξεκίνησε να καθαρίζει το
χιόνι στις 12:00 το μεσημέρι. Την πρώτη ώρα διένυσε
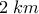 , ενώ την δεύτερη ώρα μόνο
, ενώ την δεύτερη ώρα μόνο 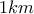 .
.Τι ώρα άρχισε να χιονίζει
 β) Μια άλλη ημέρα άρχισε πάλι να πέφτει πυκνό χιόνι με σταθερό ρυθμό (όχι κατ' ανάγκη ίσο με τον ρυθμό του
β) Μια άλλη ημέρα άρχισε πάλι να πέφτει πυκνό χιόνι με σταθερό ρυθμό (όχι κατ' ανάγκη ίσο με τον ρυθμό του(α) Ερωτήματος). Τρία (ολόιδια) εκχιονιστικά οχήματα ξεκίνησαν
διαδοχικά να καθαρίζουν το χιόνι. Το πρώτο όχημα ξεκίνησε στις 12:00 το μεσημέρι. Το δεύτερο όχημα ξεκίνησε στις 13:00
και ακολούθησε την ίδια διαδρομή που ακολούθησε και το πρώτο. Το τρίτο όχημα ξεκίνησε στις 14:00 και
ακολούθησε και αυτό την ίδια διαδρομή που ακολούθησαν τα άλλα δύο. Αν και τα τρία οχήματα συναντήθηκαν ταυτόχρονα
και στο ίδιο σημείο, τι ώρα άρχισε να χιονίζει
 Πότε συναντήθηκαν;
Πότε συναντήθηκαν;
 η συνάρτηση θέσης του εκχιονιστικού τη στιγμή
η συνάρτηση θέσης του εκχιονιστικού τη στιγμή  (σε
(σε 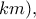
 το ύψος του χιονιού τη στιγμή
το ύψος του χιονιού τη στιγμή  (
( η ώρα που άρχισε να χιονίζει).
η ώρα που άρχισε να χιονίζει).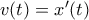 και με βάση τα δεδομένα ισχύουν
και με βάση τα δεδομένα ισχύουν 
 και αφού
και αφού  ισχύει
ισχύει






 προκύπτει
προκύπτει
![\displaystyle{x=\frac{c}{k}ln(t-t_0)-\frac{c}{k}ln(-t_0)=\frac{c}{k}[ln(t-t_0)-ln(-t_0)].} \displaystyle{x=\frac{c}{k}ln(t-t_0)-\frac{c}{k}ln(-t_0)=\frac{c}{k}[ln(t-t_0)-ln(-t_0)].}](/forum/ext/geomar/texintegr/latexrender/pictures/660e8fa3ae852796953555706ab97ab3.png)
![\displaystyle{\begin{cases} x(1)=2\\x(2)=3\end{cases} \Leftrightarrow
\begin{cases} \displaystyle{\frac{c}{k}[ln(1-t_0)-ln(-t_0)]=2} \vspace{1 mm} \\ \displaystyle{\frac{c}{k}[ln(2-t_0)-ln(-t_0)]=3} \end{cases} } \displaystyle{\begin{cases} x(1)=2\\x(2)=3\end{cases} \Leftrightarrow
\begin{cases} \displaystyle{\frac{c}{k}[ln(1-t_0)-ln(-t_0)]=2} \vspace{1 mm} \\ \displaystyle{\frac{c}{k}[ln(2-t_0)-ln(-t_0)]=3} \end{cases} }](/forum/ext/geomar/texintegr/latexrender/pictures/0cd55d7180e464ab581bd7ce554523b5.png)

![\displaystyle{ 2[ln(2-t_0)-ln(-t_0)]=3[ln(1-t_0)-ln(-t_0)] } \displaystyle{ 2[ln(2-t_0)-ln(-t_0)]=3[ln(1-t_0)-ln(-t_0)] }](/forum/ext/geomar/texintegr/latexrender/pictures/e6ad687f9ec9eacfa75f03c286134c0a.png)


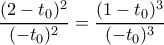




 πριν τις
πριν τις  άρχισε να χιονίζει, άρα περίπου στις
άρχισε να χιονίζει, άρα περίπου στις 
 η θέση του
η θέση του  εκχιονιστικού
εκχιονιστικού  τη στιγμή
τη στιγμή  (σε
(σε 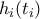 το ύψος του χιονιού που θα βρει μπροστά του το
το ύψος του χιονιού που θα βρει μπροστά του το  o χρόνος σε ώρες του
o χρόνος σε ώρες του 
 η ταχύτητα του
η ταχύτητα του 
 και
και  η χρονική στιγμή όπου
η χρονική στιγμή όπου 
 και αφού
και αφού  ισχύει
ισχύει



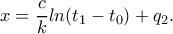




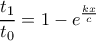

 όπου το πρώτο εκχιονιστικό περνά από το σημείο
όπου το πρώτο εκχιονιστικό περνά από το σημείο  δεν υπάρχει χιόνι και ως εκ τούτου
δεν υπάρχει χιόνι και ως εκ τούτου
 και αφού
και αφού  ισχύει
ισχύει

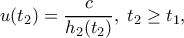


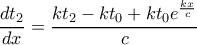

 οπότε η εξίσωση γίνεται
οπότε η εξίσωση γίνεται



 προκύπτει
προκύπτει 



 όπου το πρώτο εκχιονιστικό περνά από το σημείο
όπου το πρώτο εκχιονιστικό περνά από το σημείο 
 και αφού
και αφού  ισχύει
ισχύει










 προκύπτει
προκύπτει 




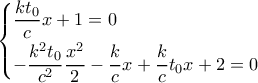




 δηλαδή στις
δηλαδή στις 