 είναι πλευρές τριγώνου, να αποδειχθεί ότι
είναι πλευρές τριγώνου, να αποδειχθεί ότι 
Συντονιστές: vittasko, achilleas, emouroukos






 =
=


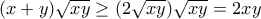 Ομοια
Ομοια 
 , ισχύει
, ισχύει 
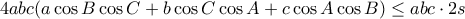

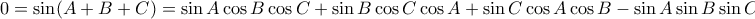
 η οποία γράφεται τελικά
η οποία γράφεται τελικά  , αφού
, αφού 
Η Ανισότητα είναι ισοδύναμη με τηνmatha έγραψε:Ανείναι πλευρές τριγώνου, να αποδειχθεί ότι
![\displaystyle{\sum [a^2-(b-c)^2]\leq \sqrt{abc}(\sqrt{a}+\sqrt{b}+\sqrt{c}),} \displaystyle{\sum [a^2-(b-c)^2]\leq \sqrt{abc}(\sqrt{a}+\sqrt{b}+\sqrt{c}),}](/forum/ext/geomar/texintegr/latexrender/pictures/f1cdb696a6b545590189d25b1a80e446.png)

![\displaystyle{a^2+b^2+c^2+a\sqrt{bc}+b\sqrt{ca}+c\sqrt{ab}\geq a^2+b^2+c^2+3\sqrt[3]{a^2b^2c^2}.} \displaystyle{a^2+b^2+c^2+a\sqrt{bc}+b\sqrt{ca}+c\sqrt{ab}\geq a^2+b^2+c^2+3\sqrt[3]{a^2b^2c^2}.}](/forum/ext/geomar/texintegr/latexrender/pictures/3d47b51b54c5990c7f36d936669e785f.png)
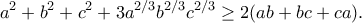



Επίσης από εδώ και κάτω είναι :G.Bas έγραψε:Η Ανισότητα είναι ισοδύναμη με τηνmatha έγραψε:Ανείναι πλευρές τριγώνου, να αποδειχθεί ότι
ή ισοδύναμα


Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες