Σελίδα 1 από 1
Συναρτησιακή ξανά
Δημοσιεύτηκε: Τετ Ιούλ 01, 2009 4:51 pm
από mathxl
Έστω η συναρτησιακή εξίσωση κ(χ+ψ)=κ(χ)+κ(ψ),χ,ψ οποιοιδήποτε πραγματικοί αριθμοί και κ συνεχής συνάρτηση,η οποία έχει ως μοναδική λύση την συνάρτηση κ(χ)=cx, c πραγματική σταθερά.
Έστω και η f(x+y)=g(x)+h(y),x,y οποιοιδήποτε πραγματικοί και f συνεχής.Nα προσδιορίσετε του τύπους των συναρτήσεων f,g,h
Re: Συναρτησιακή ξανά
Δημοσιεύτηκε: Τετ Ιούλ 01, 2009 5:20 pm
από dement
Ισχυει

για καθε

.
Αποδεικνυουμε επαγωγικα οτι ισχυει

για καθε

οποτε, αφου η

ειναι συνεχης και σταθερη στο

θα ειναι και σταθερη στο

. Αρα η

ειναι γραμμικη συναρτηση, εστω

. Ομοιως αποδεικνυουμε οτι η

ειναι επισης γραμμικη συναρτηση

και ετσι η

θα ειναι της μορφης

.
Δημητρης Σκουτερης
Re: Συναρτησιακή ξανά
Δημοσιεύτηκε: Τετ Ιούλ 01, 2009 6:18 pm
από mathxl
Εκτός από την προσέγγιση του dement, έχουμε ως λύση κάτι πιο λυκειακό; Έχω δει μία ωραία λύση(Έδωσα την cauchy για να γίνει πιο λυκειακή).
Re: Συναρτησιακή ξανά
Δημοσιεύτηκε: Πέμ Ιούλ 02, 2009 7:34 am
από R BORIS
Είναι
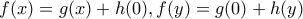
τότε

συνεχείς και επιπλέον

Αν

τότε από την προηγούμενη παίρνουμε

και επειδή w συνεχής τότε

με επαλήθευση στην αρχική σχέση

άρα

(
υπάρχει και γενίκευση θα την ανεβάσω αργότερα)
Re: Συναρτησιακή ξανά
Δημοσιεύτηκε: Πέμ Ιούλ 02, 2009 8:32 am
από R BORIS
Η γενίκευση
Να βρείτε τους τύπους όλων των συνεχών συναρτήσεων

όταν

Να σημειώσουμε ότι αρκεί η συνέχεια μόνον της f για να εξασφαλιστεί και η συνέχεια των υπολοίπων. Ο Τρόπος που είναι λυμένη στο συνημμένο είναι παρόμοιος με αυτόν που ανέβασα στο προηγούμενο post
Re: Συναρτησιακή ξανά
Δημοσιεύτηκε: Πέμ Ιούλ 02, 2009 3:05 pm
από mathxl
Η δική μου προσέγγιση μιας και δεν μπορώ να βρω από που πήρα την άσκηση ώστε αν δώσω και την λύση ...
Είναι f(x+y)=g(x)+h(y)
Για χ=0 έχουμε f(y)=g(0)+h(y), σχέση (1)
Για ψ=0 έχουμε f(x)=g(x)+h(0), σχέση (2)
Προσθέτουμε κατα μέλη τις (1) και (2): f(x)+f(y)=g(x)+h(y)+g(0)+h(0) οπότε f(x)+f(y)=f(x+y)+f(0)
Από την τελευταία αφαιρούμε από τα μέλη τον αριθμό 2f(0) και παίρνουμε
f(x+y)-f(0)=f(x)-f(0)+f(y)-f(0), σχέση (3). Θεωρούμε την συνάρτηση κ(χ)=f(x)-f(0),σχέση (4)
Οπότε η σχέση (3) μετασχηματίζεται στην k(x+y)=k(x)+k(y) από υπόθεση θα είναι k(x)=cx
Από (4) παίρνουμε f(x)=cx+f(0)
Από (1) παίρνουμε h(y)=cy+f(0)-g(0)=cy+h(0)
Από (2) παίρνουμε g(x)= cx+f(0)-h(0)=cx+g(0)
Πάντως η λύση που είχα δει ξεκινούσε κάπως έτσι
Για ψ=χ και χ=ψ : f(y+x)=g(y)+h(x) άρα g(y)+h(x)=g(x)+h(y) οπότε g(x)-h(x)=g(y)-h(y)= σταθερό κτλ...
 για καθε
για καθε  .
. για καθε
για καθε  οποτε, αφου η
οποτε, αφου η  ειναι συνεχης και σταθερη στο
ειναι συνεχης και σταθερη στο  θα ειναι και σταθερη στο
θα ειναι και σταθερη στο  . Αρα η
. Αρα η  ειναι γραμμικη συναρτηση, εστω
ειναι γραμμικη συναρτηση, εστω  . Ομοιως αποδεικνυουμε οτι η
. Ομοιως αποδεικνυουμε οτι η  ειναι επισης γραμμικη συναρτηση
ειναι επισης γραμμικη συναρτηση  και ετσι η
και ετσι η  θα ειναι της μορφης
θα ειναι της μορφης  .
.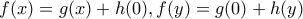 τότε
τότε  συνεχείς και επιπλέον
συνεχείς και επιπλέον 
 τότε από την προηγούμενη παίρνουμε
τότε από την προηγούμενη παίρνουμε  και επειδή w συνεχής τότε
και επειδή w συνεχής τότε 
 άρα
άρα 
 όταν
όταν 