Συναρτησιακή ξανά
Συντονιστής: m.pαpαgrigorakis
Συναρτησιακή ξανά
Έστω η συναρτησιακή εξίσωση κ(χ+ψ)=κ(χ)+κ(ψ),χ,ψ οποιοιδήποτε πραγματικοί αριθμοί και κ συνεχής συνάρτηση,η οποία έχει ως μοναδική λύση την συνάρτηση κ(χ)=cx, c πραγματική σταθερά.
Έστω και η f(x+y)=g(x)+h(y),x,y οποιοιδήποτε πραγματικοί και f συνεχής.Nα προσδιορίσετε του τύπους των συναρτήσεων f,g,h
Έστω και η f(x+y)=g(x)+h(y),x,y οποιοιδήποτε πραγματικοί και f συνεχής.Nα προσδιορίσετε του τύπους των συναρτήσεων f,g,h
Ποτε δεν κάνω λάθος! Μια φορά νομιζα πως είχα κάνει, αλλά τελικά έκανα λάθος!
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Re: Συναρτησιακή ξανά
Ισχυει  για καθε
για καθε  .
.
Αποδεικνυουμε επαγωγικα οτι ισχυει για καθε
για καθε  οποτε, αφου η
οποτε, αφου η  ειναι συνεχης και σταθερη στο
ειναι συνεχης και σταθερη στο  θα ειναι και σταθερη στο
θα ειναι και σταθερη στο  . Αρα η
. Αρα η  ειναι γραμμικη συναρτηση, εστω
ειναι γραμμικη συναρτηση, εστω  . Ομοιως αποδεικνυουμε οτι η
. Ομοιως αποδεικνυουμε οτι η  ειναι επισης γραμμικη συναρτηση
ειναι επισης γραμμικη συναρτηση  και ετσι η
και ετσι η  θα ειναι της μορφης
θα ειναι της μορφης  .
.
Δημητρης Σκουτερης
 για καθε
για καθε  .
.Αποδεικνυουμε επαγωγικα οτι ισχυει
 για καθε
για καθε  οποτε, αφου η
οποτε, αφου η  ειναι συνεχης και σταθερη στο
ειναι συνεχης και σταθερη στο  θα ειναι και σταθερη στο
θα ειναι και σταθερη στο  . Αρα η
. Αρα η  ειναι γραμμικη συναρτηση, εστω
ειναι γραμμικη συναρτηση, εστω  . Ομοιως αποδεικνυουμε οτι η
. Ομοιως αποδεικνυουμε οτι η  ειναι επισης γραμμικη συναρτηση
ειναι επισης γραμμικη συναρτηση  και ετσι η
και ετσι η  θα ειναι της μορφης
θα ειναι της μορφης  .
.Δημητρης Σκουτερης
Δημήτρης Σκουτέρης
Τα μαθηματικά είναι η μοναδική επιστήμη που θα μπορούσε κανείς να εξακολουθήσει να ασκεί αν κάποτε ξυπνούσε και το σύμπαν δεν υπήρχε πλέον.
Τα μαθηματικά είναι η μοναδική επιστήμη που θα μπορούσε κανείς να εξακολουθήσει να ασκεί αν κάποτε ξυπνούσε και το σύμπαν δεν υπήρχε πλέον.
Re: Συναρτησιακή ξανά
Εκτός από την προσέγγιση του dement, έχουμε ως λύση κάτι πιο λυκειακό; Έχω δει μία ωραία λύση(Έδωσα την cauchy για να γίνει πιο λυκειακή).
Ποτε δεν κάνω λάθος! Μια φορά νομιζα πως είχα κάνει, αλλά τελικά έκανα λάθος!
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Re: Συναρτησιακή ξανά
Είναι 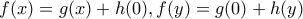 τότε
τότε  συνεχείς και επιπλέον
συνεχείς και επιπλέον 
Αν τότε από την προηγούμενη παίρνουμε
τότε από την προηγούμενη παίρνουμε  και επειδή w συνεχής τότε
και επειδή w συνεχής τότε 
με επαλήθευση στην αρχική σχέση άρα
άρα 
(υπάρχει και γενίκευση θα την ανεβάσω αργότερα)
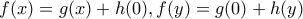 τότε
τότε  συνεχείς και επιπλέον
συνεχείς και επιπλέον 
Αν
 τότε από την προηγούμενη παίρνουμε
τότε από την προηγούμενη παίρνουμε  και επειδή w συνεχής τότε
και επειδή w συνεχής τότε 
με επαλήθευση στην αρχική σχέση
 άρα
άρα 
(υπάρχει και γενίκευση θα την ανεβάσω αργότερα)
Re: Συναρτησιακή ξανά
Η γενίκευση
Να βρείτε τους τύπους όλων των συνεχών συναρτήσεων όταν
όταν 
Να σημειώσουμε ότι αρκεί η συνέχεια μόνον της f για να εξασφαλιστεί και η συνέχεια των υπολοίπων. Ο Τρόπος που είναι λυμένη στο συνημμένο είναι παρόμοιος με αυτόν που ανέβασα στο προηγούμενο post
Να βρείτε τους τύπους όλων των συνεχών συναρτήσεων
 όταν
όταν 
Να σημειώσουμε ότι αρκεί η συνέχεια μόνον της f για να εξασφαλιστεί και η συνέχεια των υπολοίπων. Ο Τρόπος που είναι λυμένη στο συνημμένο είναι παρόμοιος με αυτόν που ανέβασα στο προηγούμενο post
- Συνημμένα
-
- forum 79.doc
- (39 KiB) Μεταφορτώθηκε 52 φορές
Re: Συναρτησιακή ξανά
Η δική μου προσέγγιση μιας και δεν μπορώ να βρω από που πήρα την άσκηση ώστε αν δώσω και την λύση ...
Είναι f(x+y)=g(x)+h(y)
Για χ=0 έχουμε f(y)=g(0)+h(y), σχέση (1)
Για ψ=0 έχουμε f(x)=g(x)+h(0), σχέση (2)
Προσθέτουμε κατα μέλη τις (1) και (2): f(x)+f(y)=g(x)+h(y)+g(0)+h(0) οπότε f(x)+f(y)=f(x+y)+f(0)
Από την τελευταία αφαιρούμε από τα μέλη τον αριθμό 2f(0) και παίρνουμε
f(x+y)-f(0)=f(x)-f(0)+f(y)-f(0), σχέση (3). Θεωρούμε την συνάρτηση κ(χ)=f(x)-f(0),σχέση (4)
Οπότε η σχέση (3) μετασχηματίζεται στην k(x+y)=k(x)+k(y) από υπόθεση θα είναι k(x)=cx
Από (4) παίρνουμε f(x)=cx+f(0)
Από (1) παίρνουμε h(y)=cy+f(0)-g(0)=cy+h(0)
Από (2) παίρνουμε g(x)= cx+f(0)-h(0)=cx+g(0)
Πάντως η λύση που είχα δει ξεκινούσε κάπως έτσι
Για ψ=χ και χ=ψ : f(y+x)=g(y)+h(x) άρα g(y)+h(x)=g(x)+h(y) οπότε g(x)-h(x)=g(y)-h(y)= σταθερό κτλ...
Είναι f(x+y)=g(x)+h(y)
Για χ=0 έχουμε f(y)=g(0)+h(y), σχέση (1)
Για ψ=0 έχουμε f(x)=g(x)+h(0), σχέση (2)
Προσθέτουμε κατα μέλη τις (1) και (2): f(x)+f(y)=g(x)+h(y)+g(0)+h(0) οπότε f(x)+f(y)=f(x+y)+f(0)
Από την τελευταία αφαιρούμε από τα μέλη τον αριθμό 2f(0) και παίρνουμε
f(x+y)-f(0)=f(x)-f(0)+f(y)-f(0), σχέση (3). Θεωρούμε την συνάρτηση κ(χ)=f(x)-f(0),σχέση (4)
Οπότε η σχέση (3) μετασχηματίζεται στην k(x+y)=k(x)+k(y) από υπόθεση θα είναι k(x)=cx
Από (4) παίρνουμε f(x)=cx+f(0)
Από (1) παίρνουμε h(y)=cy+f(0)-g(0)=cy+h(0)
Από (2) παίρνουμε g(x)= cx+f(0)-h(0)=cx+g(0)
Πάντως η λύση που είχα δει ξεκινούσε κάπως έτσι
Για ψ=χ και χ=ψ : f(y+x)=g(y)+h(x) άρα g(y)+h(x)=g(x)+h(y) οπότε g(x)-h(x)=g(y)-h(y)= σταθερό κτλ...
Ποτε δεν κάνω λάθος! Μια φορά νομιζα πως είχα κάνει, αλλά τελικά έκανα λάθος!
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες
