Σελίδα 1 από 1
Δύο οριάκια
Δημοσιεύτηκε: Τετ Οκτ 05, 2011 2:25 pm
από irakleios
Να υπολογισθούν :
A)  B)
B) 
Re: Δύο οριάκια
Δημοσιεύτηκε: Τετ Οκτ 05, 2011 2:52 pm
από matha
irakleios έγραψε:Να υπολογισθούν :
A)  B)
B) 
α)
Για αρκετά μεγάλο

(π.χ.

) είναι

(εύκολο)
άρα είναι τότε,

, οπότε

Από το κριτήριο παρεμβολής προκύπτει

άρα
 β)
β) Εύκολα βλέπουμε, ότι για μεγάλο

είναι

και από το κριτήριο παρεμβολής, το ζητούμενο όριο ισούται με

Re: Δύο οριάκια
Δημοσιεύτηκε: Τετ Οκτ 05, 2011 4:37 pm
από Mihalis_Lambrou
irakleios έγραψε:Να υπολογισθούν :
A)  B)
B) 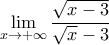
Αλλιώς:
Α) Με l' Hospital βρίσκουμε ότι

.
Άρα

(ως άπειρο επί άπειρο)
Β)

Φιλικά,
Μιχάλης
Re: Δύο οριάκια
Δημοσιεύτηκε: Τετ Οκτ 05, 2011 4:38 pm
από Νίκος Ζαφειρόπουλος






 (π.χ.
(π.χ.  ) είναι
) είναι  (εύκολο)
(εύκολο) , οπότε
, οπότε  Από το κριτήριο παρεμβολής προκύπτει
Από το κριτήριο παρεμβολής προκύπτει  άρα
άρα 
 είναι
είναι 

 .
. (ως άπειρο επί άπειρο)
(ως άπειρο επί άπειρο)
 ,γιατί
,γιατί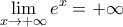 και
και

