 , συνεχής στα 0 και 1 για την οποία ισχύει
, συνεχής στα 0 και 1 για την οποία ισχύει 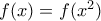 για κάθε
για κάθε  πραγματικό. Να βρεθεί ο τύπος της
πραγματικό. Να βρεθεί ο τύπος της  .
.Συντονιστής: m.pαpαgrigorakis
 , συνεχής στα 0 και 1 για την οποία ισχύει
, συνεχής στα 0 και 1 για την οποία ισχύει 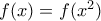 για κάθε
για κάθε  πραγματικό. Να βρεθεί ο τύπος της
πραγματικό. Να βρεθεί ο τύπος της  .
.Απάντηση: Είναι σταθερή. Πρώτα δείχνουμε ότι είναι σταθερή στοpito έγραψε:Έστω η συνάρτηση, συνεχής στα 0 και 1 για την οποία ισχύει
για κάθε
πραγματικό. Να βρεθεί ο τύπος της
.
 και επίσης σταθερή (ενδεχομένως με άλλη τιμή) στο
και επίσης σταθερή (ενδεχομένως με άλλη τιμή) στο ![(-\infty, \, -1] \cup [1, \infty) (-\infty, \, -1] \cup [1, \infty)](/forum/ext/geomar/texintegr/latexrender/pictures/51518ab44b4f818ca1621f6091d3a73f.png) . Τέλος, λόγω συνέχειας στο
. Τέλος, λόγω συνέχειας στο  οι δύο στεθερές συμπίπτουν.
οι δύο στεθερές συμπίπτουν. . Τότε η ακολουθία
. Τότε η ακολουθία  συγκλίνει στο
συγκλίνει στο  . Αλλά εξ υποθέσεως
. Αλλά εξ υποθέσεως  . Άρα
. Άρα  . Όμοια αν
. Όμοια αν  αλλά τώρα εξετάζουμε τα
αλλά τώρα εξετάζουμε τα ![a, \sqrt a, \sqrt[4] a, ... a, \sqrt a, \sqrt[4] a, ...](/forum/ext/geomar/texintegr/latexrender/pictures/ebda817089796aba7d1aeb95b31277c1.png) που συγκλίνουν στο
που συγκλίνουν στο  και
και ![f(a)= f(\sqrt a)= f(\sqrt[4] a) = ... = f(\sqrt[2^n]{a})= ... \to f(1) f(a)= f(\sqrt a)= f(\sqrt[4] a) = ... = f(\sqrt[2^n]{a})= ... \to f(1)](/forum/ext/geomar/texintegr/latexrender/pictures/5c7d94b0916ebfb9c41951208246a2ee.png) .
. έχουν τις τιμές που αναφέραμε γιατί
έχουν τις τιμές που αναφέραμε γιατί  ,
,  και τα
και τα  είναι συγχρόνως μικρότερα ή μεγαλύτερα του
είναι συγχρόνως μικρότερα ή μεγαλύτερα του  .
. για κάθε
για κάθε 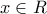 θα ισχύει
θα ισχύει  άρα και
άρα και 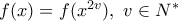
 επειδή
επειδή  και
και  συνεχής στο
συνεχής στο  θα ισχύει
θα ισχύει 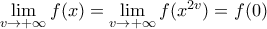 άρα
άρα  ,
, 
 ισχύει
ισχύει  άρα και
άρα και ![f(\sqrt[2v]{x})=...=f(\sqrt[4]{x})=f(\sqrt{x})=f(x) f(\sqrt[2v]{x})=...=f(\sqrt[4]{x})=f(\sqrt{x})=f(x)](/forum/ext/geomar/texintegr/latexrender/pictures/9c907a0e4cd934ec9b1402a2267e27ee.png) θα είναι
θα είναι  με
με 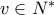 Για
Για  επειδή
επειδή 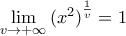 και και
και και 
 θα ισχύει
θα ισχύει  άρα
άρα 
 επομένως η
επομένως η 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες