 τέτοια ώστε
τέτοια ώστε  για κάθε
για κάθε 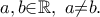
Συντονιστής: m.pαpαgrigorakis
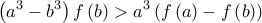

 με
με  .
.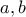 στη σχέση
στη σχέση  έχουμε ότι:
έχουμε ότι:

 με
με  .
. με
με  τέτοια, ώστε
τέτοια, ώστε 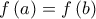 . Τότε, από τις σχέσεις
. Τότε, από τις σχέσεις  και
και  προκύπτει ότι:
προκύπτει ότι: και
και 
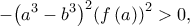
 είναι 1-1.
είναι 1-1.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες