Σελίδα 1 από 1
Περιττή και Αντιστρέψιμη
Δημοσιεύτηκε: Τρί Αύγ 07, 2012 3:05 am
από gian7
Έστω πραγματική συνάρτηση

η οποία είναι περιττή και αντιστρέψιμη. Να δείξετε ότι και η αντίστροφή της είναι περιττή.
Re: Περιττή και Αντιστρέψιμη
Δημοσιεύτηκε: Τρί Αύγ 07, 2012 3:18 am
από cretanman
Ας υποθέσουμε

η συνάρτηση για την οποία ισχύουν οι σχέσεις:
i) για κάθε

είναι

και
ii)

για κάθε
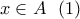
.
Θεωρούμε τυχαίο

. Τότε αφού η συνάρτηση είναι αντιστρέψιμη, άρα υπάρχει μοναδικό

ώστε

και από την

παίρνουμε

δηλαδή

οπότε

(διότι υπάρχει το

ώστε

).
Από την άλλη αφού

άρα

και αφού

άρα

. Συνδυάζοντας τις δύο τελευταίες έχουμε

για κάθε

.
Άρα η

είναι περιττή.
Αλέξανδρος
Re: Περιττή και Αντιστρέψιμη
Δημοσιεύτηκε: Τρί Αύγ 07, 2012 4:22 am
από parmenides51
το συμμετρικό

ενός σχήματος

που έχει κέντρο συμμετρίας

, ως προς μια ευθεία

είναι σχήμα με κέντρο συμμετρίας το σημείο

, το συμμετρικό του

ως προς την ευθεία
 και τα σημεία της ευθείας
και τα σημεία της ευθείας  είναι σταθερά σημεία κατά τον μετασχηματισμό συμμετρίας ως προς την ευθεία
είναι σταθερά σημεία κατά τον μετασχηματισμό συμμετρίας ως προς την ευθεία 
κι
εδώ
 η οποία είναι περιττή και αντιστρέψιμη. Να δείξετε ότι και η αντίστροφή της είναι περιττή.
η οποία είναι περιττή και αντιστρέψιμη. Να δείξετε ότι και η αντίστροφή της είναι περιττή. η οποία είναι περιττή και αντιστρέψιμη. Να δείξετε ότι και η αντίστροφή της είναι περιττή.
η οποία είναι περιττή και αντιστρέψιμη. Να δείξετε ότι και η αντίστροφή της είναι περιττή. η συνάρτηση για την οποία ισχύουν οι σχέσεις:
η συνάρτηση για την οποία ισχύουν οι σχέσεις: είναι
είναι  και
και για κάθε
για κάθε 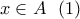 .
. . Τότε αφού η συνάρτηση είναι αντιστρέψιμη, άρα υπάρχει μοναδικό
. Τότε αφού η συνάρτηση είναι αντιστρέψιμη, άρα υπάρχει μοναδικό  ώστε
ώστε  και από την
και από την  παίρνουμε
παίρνουμε  δηλαδή
δηλαδή  οπότε
οπότε  (διότι υπάρχει το
(διότι υπάρχει το  ώστε
ώστε  και αφού
και αφού  . Συνδυάζοντας τις δύο τελευταίες έχουμε
. Συνδυάζοντας τις δύο τελευταίες έχουμε  για κάθε
για κάθε  είναι περιττή.
είναι περιττή. ενός σχήματος
ενός σχήματος  που έχει κέντρο συμμετρίας
που έχει κέντρο συμμετρίας  , ως προς μια ευθεία
, ως προς μια ευθεία  είναι σχήμα με κέντρο συμμετρίας το σημείο
είναι σχήμα με κέντρο συμμετρίας το σημείο  , το συμμετρικό του
, το συμμετρικό του