erxmer έγραψε:Θεωρούμε τις συνεχείς συναρτήσεις
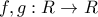
ώστε:

Δ1. Να δείξετε ότι

για κάθε

Δ2. Να δείξετε ότι

Δ3. Να βρείτε τη μονοτονία της συνάρτησης

.
Δ4. Να βρείτε το σύνολο τιμών της

και να δείξετε ότι η

έχει ακριβώς 2 ετερόσημες ρίζες .
Δ5. Να δείξετε ότι η εξίσωση

έχει μια τουλάχιστον ρίζα στο διάστημα

, για κάθε

Καλησπέρα. Μια προσπάθεια...
Δ1. Είναι:

\displaystyle{\Leftrightarrow}

Θεωρώ την

Ισχύει

συνεχής στο

και

.
Συνεπώς η

διατηρεί πρόσημο στο

και αφού

συμπεραίνουμε ότι και

.
Άρα



.
Δ2.

συνεχής στο



Έχουμε

Επίσης πρέπει


![\displaystyle\lim_{x\to 0^+} [a-2x-ln(x+1)] =1 \displaystyle\lim_{x\to 0^+} [a-2x-ln(x+1)] =1](/forum/ext/geomar/texintegr/latexrender/pictures/2bbdd37de50d16b0aa1a55ccda4cab4e.png)


Δ3.
![\forall x_{1},χ_{2} \in (-\infty , 0] \forall x_{1},χ_{2} \in (-\infty , 0]](/forum/ext/geomar/texintegr/latexrender/pictures/128b25b94a1d84d9ee25e51a3f26a85e.png)
με



. Αρα με πρόσθεση κατά μέλη των δύο ανισοτήτων προκύπτει:

δηλαδή

, συνεπώς

γνησίως αύξουσα στο
![(-\infty , 0] (-\infty , 0]](/forum/ext/geomar/texintegr/latexrender/pictures/a066ce007d5aab553bb0153b730293ff.png)
.
Επίσης

με



.
Επίσης



. Από τις παραπάνω ανισότητες προκύπτει

, συνεπώς

γνησίως φθίνουσα στο

.
Δ4. Είναι

και

. Αφού

γνησίως αύξουσα και συνεχής στο
![(-\infty , 0] (-\infty , 0]](/forum/ext/geomar/texintegr/latexrender/pictures/a066ce007d5aab553bb0153b730293ff.png)
,
![g((-\infty , 0])=(-\infty , 1] g((-\infty , 0])=(-\infty , 1]](/forum/ext/geomar/texintegr/latexrender/pictures/b79606af89f97f651972ccee54a980e3.png)
.
Ισχύει
![0\in(-\infty , 1] 0\in(-\infty , 1]](/forum/ext/geomar/texintegr/latexrender/pictures/a34efc8dc1649ea20172c5b3885f6c62.png)
άρα υπάρχει μοναδικό, λόγω μονοτονίας,
![x_{1}\in(-\infty , 0] x_{1}\in(-\infty , 0]](/forum/ext/geomar/texintegr/latexrender/pictures/78003705189b3f90b09b319afa2d8ea1.png)
ώστε

Επιπλέον

και

. Αφού

γνησίως φθίνουσα και συνεχής στο

,

.
Ισχύει

άρα υπάρχει μοναδικό, λόγω μονοτονίας,

ώστε

.
Δ5. Η εξίσωση ισοδυνάμως γράφεται:
![(x-2)[g(c)-1] +(x-1)[g(d)-1]-2017(x-1)(x-2)=0 (x-2)[g(c)-1] +(x-1)[g(d)-1]-2017(x-1)(x-2)=0](/forum/ext/geomar/texintegr/latexrender/pictures/37db875c176f4af64b0e08bceda537ce.png)

Θεωρώντας την συνεχή στο
![[1,2] [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/f79408e5ca998cd53faf44af31e6eb45.png)
![r(x)= (x-2)[g(c)-1] +(x-1)[g(d)-1]-2017(x-1)(x-2) r(x)= (x-2)[g(c)-1] +(x-1)[g(d)-1]-2017(x-1)(x-2)](/forum/ext/geomar/texintegr/latexrender/pictures/e74144f9a64e87daaa82bc632c3da4b6.png)
έχουμε
![r(1) r(2) = -[g(c)-1][g(d)-1]<0 r(1) r(2) = -[g(c)-1][g(d)-1]<0](/forum/ext/geomar/texintegr/latexrender/pictures/748cef4c0298461183be5683ed5b5df3.png)
αφού

και

.
Συνεπώς από Θ. Bolzano υπάρχει μία τουλάχιστον ρίζα στο

.
Φιλικά
Σταμ. Γλάρος
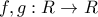 ώστε:
ώστε: 
 για κάθε
για κάθε 

 .
.  και να δείξετε ότι η
και να δείξετε ότι η  έχει ακριβώς 2 ετερόσημες ρίζες .
έχει ακριβώς 2 ετερόσημες ρίζες . έχει μια τουλάχιστον ρίζα στο διάστημα
έχει μια τουλάχιστον ρίζα στο διάστημα  , για κάθε
, για κάθε 

 \displaystyle{\Leftrightarrow}
\displaystyle{\Leftrightarrow}
 Ισχύει
Ισχύει  συνεχής στο
συνεχής στο  και
και  .
. διατηρεί πρόσημο στο
διατηρεί πρόσημο στο  συμπεραίνουμε ότι και
συμπεραίνουμε ότι και  .
.

 .
. συνεχής στο
συνεχής στο 



![\displaystyle\lim_{x\to 0^+} [a-2x-ln(x+1)] =1 \displaystyle\lim_{x\to 0^+} [a-2x-ln(x+1)] =1](/forum/ext/geomar/texintegr/latexrender/pictures/2bbdd37de50d16b0aa1a55ccda4cab4e.png)

![\forall x_{1},χ_{2} \in (-\infty , 0] \forall x_{1},χ_{2} \in (-\infty , 0]](/forum/ext/geomar/texintegr/latexrender/pictures/128b25b94a1d84d9ee25e51a3f26a85e.png) με
με 

 . Αρα με πρόσθεση κατά μέλη των δύο ανισοτήτων προκύπτει:
. Αρα με πρόσθεση κατά μέλη των δύο ανισοτήτων προκύπτει: δηλαδή
δηλαδή  , συνεπώς
, συνεπώς ![(-\infty , 0] (-\infty , 0]](/forum/ext/geomar/texintegr/latexrender/pictures/a066ce007d5aab553bb0153b730293ff.png) .
. με
με  .
. . Από τις παραπάνω ανισότητες προκύπτει
. Από τις παραπάνω ανισότητες προκύπτει  , συνεπώς
, συνεπώς  .
. και
και  . Αφού
. Αφού ![g((-\infty , 0])=(-\infty , 1] g((-\infty , 0])=(-\infty , 1]](/forum/ext/geomar/texintegr/latexrender/pictures/b79606af89f97f651972ccee54a980e3.png) .
. ![0\in(-\infty , 1] 0\in(-\infty , 1]](/forum/ext/geomar/texintegr/latexrender/pictures/a34efc8dc1649ea20172c5b3885f6c62.png) άρα υπάρχει μοναδικό, λόγω μονοτονίας,
άρα υπάρχει μοναδικό, λόγω μονοτονίας, ![x_{1}\in(-\infty , 0] x_{1}\in(-\infty , 0]](/forum/ext/geomar/texintegr/latexrender/pictures/78003705189b3f90b09b319afa2d8ea1.png) ώστε
ώστε 
 και
και  . Αφού
. Αφού  .
. άρα υπάρχει μοναδικό, λόγω μονοτονίας,
άρα υπάρχει μοναδικό, λόγω μονοτονίας,  ώστε
ώστε  .
.![(x-2)[g(c)-1] +(x-1)[g(d)-1]-2017(x-1)(x-2)=0 (x-2)[g(c)-1] +(x-1)[g(d)-1]-2017(x-1)(x-2)=0](/forum/ext/geomar/texintegr/latexrender/pictures/37db875c176f4af64b0e08bceda537ce.png)
![[1,2] [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/f79408e5ca998cd53faf44af31e6eb45.png)
![r(x)= (x-2)[g(c)-1] +(x-1)[g(d)-1]-2017(x-1)(x-2) r(x)= (x-2)[g(c)-1] +(x-1)[g(d)-1]-2017(x-1)(x-2)](/forum/ext/geomar/texintegr/latexrender/pictures/e74144f9a64e87daaa82bc632c3da4b6.png) έχουμε
έχουμε ![r(1) r(2) = -[g(c)-1][g(d)-1]<0 r(1) r(2) = -[g(c)-1][g(d)-1]<0](/forum/ext/geomar/texintegr/latexrender/pictures/748cef4c0298461183be5683ed5b5df3.png) αφού
αφού  και
και  .
.