 και
και 
α) Να βρείτε τα πεδία ορισμού τους και να δείξετε ότι η
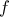 είναι άρτια .
είναι άρτια .β) Να δείξετε ότι
 και κατόπιν να βρείτε το σύνολο τιμών της
και κατόπιν να βρείτε το σύνολο τιμών της 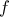 .
.γ) Να μελετήσετε τη μονοτονία της
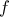 .
.δ) Να ορίσετε την αντίστροφη της

Συντονιστής: m.pαpαgrigorakis
 και
και 
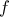 είναι άρτια .
είναι άρτια . και κατόπιν να βρείτε το σύνολο τιμών της
και κατόπιν να βρείτε το σύνολο τιμών της 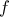 .
.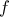 .
.
γειά σου Γιώργη...μιά προσπάθεια με ψυχραιμία....
 πρέπει και αρκεί
πρέπει και αρκεί  άρα το πεδίο ορισμού της
άρα το πεδίο ορισμού της  είναι το
είναι το  και για να ορίζεται η
και για να ορίζεται η  πρέπει και αρκεί για
πρέπει και αρκεί για  το
το  και
και  και
και  που ισοδύναμα έχουμε
που ισοδύναμα έχουμε  και
και  και
και  και
και  και τελικά
και τελικά  επομένως πεδίο ορισμού της
επομένως πεδίο ορισμού της  είναι το διάστημα
είναι το διάστημα 
 το
το  και
και 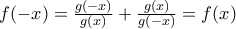 άρα η
άρα η 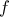 είναι άρτια .
είναι άρτια . (1)
(1)  και αφού
και αφού  για κάθε
για κάθε  και για κάθε
και για κάθε  η (1) ισχύει
η (1) ισχύει  και άρα
και άρα  επομένως η συνάρτηση
επομένως η συνάρτηση 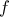 έχει ελάχιστη τιμή το
έχει ελάχιστη τιμή το  και επειδή
και επειδή 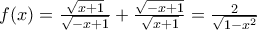 και
και  και
και 
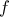 είναι το σύνολο
είναι το σύνολο 
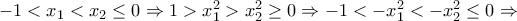

 άρα η
άρα η  είναι γνήσια φθίνουσα στο
είναι γνήσια φθίνουσα στο ![(-1,\,0] (-1,\,0]](/forum/ext/geomar/texintegr/latexrender/pictures/22d84ed8c88a3d8b57aae483dfc11b55.png) και με ανάλογο τρόπο δείχνουμε για
και με ανάλογο τρόπο δείχνουμε για 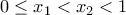 ότι η
ότι η  είναι γνήσια αύξουσα στο
είναι γνήσια αύξουσα στο 
 πρέπει να υπάρχουν
πρέπει να υπάρχουν 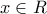 που
που  και
και  επομένως πεδίο ορισμού της
επομένως πεδίο ορισμού της  είναι το διάστημα
είναι το διάστημα  και επιπλέον για
και επιπλέον για  με
με  και
και  και
και 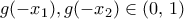 που η
που η  είναι γνήσια αύξουσα άρα και
είναι γνήσια αύξουσα άρα και  προκύπτει ότι
προκύπτει ότι  ( η
( η  είναι γνήσια αύξουσα στο πεδίο ορισμού της )
είναι γνήσια αύξουσα στο πεδίο ορισμού της )  είναι αντιστρέψιμη με
είναι αντιστρέψιμη με  και αφού για
και αφού για  ή
ή  δηλαδή
δηλαδή 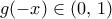
 είναι
είναι  επομένως
επομένως  και επειδή
και επειδή  και
και  είναι
είναι 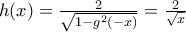
 έχουμε από
έχουμε από  δηλαδή
δηλαδή 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες