Η συνάρτηση
 είναι γνησίως μονότονη και ισχύει
είναι γνησίως μονότονη και ισχύει 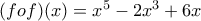 για κάθε
για κάθε  πραγματικό. Να δείξετε ότι οι γραφικές παραστάσεις των
πραγματικό. Να δείξετε ότι οι γραφικές παραστάσεις των  έχουν ένα μόνο κοινό σημείο.
έχουν ένα μόνο κοινό σημείο.Συντονιστής: m.pαpαgrigorakis
 είναι γνησίως μονότονη και ισχύει
είναι γνησίως μονότονη και ισχύει 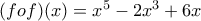 για κάθε
για κάθε  πραγματικό. Να δείξετε ότι οι γραφικές παραστάσεις των
πραγματικό. Να δείξετε ότι οι γραφικές παραστάσεις των  έχουν ένα μόνο κοινό σημείο.
έχουν ένα μόνο κοινό σημείο.Καλησπέρα Μυρτώ.
 . Για να το πετύχουμε αυτό πρέπει
. Για να το πετύχουμε αυτό πρέπει  στο
στο  Δείχνουμε ότι η αντίστροφη
Δείχνουμε ότι η αντίστροφη  έχει πεδίο ορισμού το
έχει πεδίο ορισμού το 
 έχει σύνολο τιμών το
έχει σύνολο τιμών το  . Πράγματι, έστω ότι δεν έχει σύνολο τιμών το
. Πράγματι, έστω ότι δεν έχει σύνολο τιμών το  .
.  τέτοιο, ώστε
τέτοιο, ώστε 
 ως γνησίως μονότονη θα είναι και 1-1. Η τελευταία σχέση όμως μας
ως γνησίως μονότονη θα είναι και 1-1. Η τελευταία σχέση όμως μας  είναι κάποιος πραγματικός και μας λέει ουσιαστικά ότι αυτός δεν ανήκει στο σύνολο τιμών της
είναι κάποιος πραγματικός και μας λέει ουσιαστικά ότι αυτός δεν ανήκει στο σύνολο τιμών της  η οποία όμως εύκολα ελέγχουμε ότι έχει σύνολο τιμών το
η οποία όμως εύκολα ελέγχουμε ότι έχει σύνολο τιμών το 
 .
.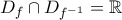 και έχουμε
και έχουμε 

 είναι συνάρτηση
είναι συνάρτηση  και 1-1
και 1-1  .
. ως εξής: Παρατηρούμε ότι η εξίσωση
ως εξής: Παρατηρούμε ότι η εξίσωση  έχει μοναδική λύση στο
έχει μοναδική λύση στο  την
την  Αυτή θα είναι η μοναδική λύση της
Αυτή θα είναι η μοναδική λύση της στο
στο 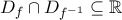 αρκεί
αρκεί 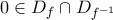 . Όμως
. Όμως  και
και 
 τέτοιο, ώστε
τέτοιο, ώστε  . Άρα
. Άρα  .Τελικά
.Τελικά  .
....μια αντιμετώπιση...εντός φακέλλου...
 και επειδή είναι
και επειδή είναι 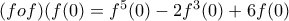 θα είναι
θα είναι 
 γιατί
γιατί  έτσι λόγω
έτσι λόγω  άρα οι γραφικές παραστάσεις των
άρα οι γραφικές παραστάσεις των  έχουν ένα κοινό σημείο το
έχουν ένα κοινό σημείο το 
 που
που  τότε
τότε 
 γιατί
γιατί  που είναι άτοπο
που είναι άτοπο  έχουν ένα μόνο ένα κοινό σημείο το
έχουν ένα μόνο ένα κοινό σημείο το 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες