 , για τις οποίες έχει λύση η εξίσωση
, για τις οποίες έχει λύση η εξίσωση .
.Συντονιστής: m.pαpαgrigorakis
 , για τις οποίες έχει λύση η εξίσωση
, για τις οποίες έχει λύση η εξίσωση .
.Al.Koutsouridis έγραψε: ↑Τετ Ιαν 02, 2019 12:44 pmΝα βρείτε τις τιμές της παραμέτρου, για τις οποίες έχει λύση η εξίσωση
.
 . Πρέπει
. Πρέπει  Ακόμα είναι
Ακόμα είναι  οπότε
οπότε  . Επομένως
. Επομένως 
 Η εξίσωση γράφεται
Η εξίσωση γράφεται  . Υψώνουμε τις δύο ισότητες αυτές στο τετράγωνο, τις αφαιρούμε κατά μέλη και γρήγορα προκύπτει
. Υψώνουμε τις δύο ισότητες αυτές στο τετράγωνο, τις αφαιρούμε κατά μέλη και γρήγορα προκύπτει
 αποκλείεται αφού
αποκλείεται αφού  , άρα
, άρα 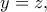 οπότε
οπότε  Είναι, όμως
Είναι, όμως
 να έχει λύση στο διάστημα
να έχει λύση στο διάστημα ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) . Για αρχή, η διακρίνουσα είναι μη αρνητική:
. Για αρχή, η διακρίνουσα είναι μη αρνητική:
 και εξετάζουμε τις σχετικές θέσεις των αριθμών
και εξετάζουμε τις σχετικές θέσεις των αριθμών  , ως προς τις τις ρίζες
, ως προς τις τις ρίζες  της g. Θα μας βοηθήσει το θεώρημα που αναφέρεται στο πρόσημο των τιμών τριωνύμου.
της g. Θα μας βοηθήσει το θεώρημα που αναφέρεται στο πρόσημο των τιμών τριωνύμου.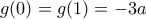 και τώρα:
και τώρα: τότε τα
τότε τα  και
και  βρίσκονται εντός του διαστήματος των ριζών, γιατί
βρίσκονται εντός του διαστήματος των ριζών, γιατί  , (τιμές ετερόσημες του συντελεστή του
, (τιμές ετερόσημες του συντελεστή του  ), με άλλα λόγια οι ρίζες δεν βρίσκονται στο διάστημα
), με άλλα λόγια οι ρίζες δεν βρίσκονται στο διάστημα ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) και η περίπτωση αποκλείεται.
και η περίπτωση αποκλείεται. , τότε οι ρίζες βρίσκονται στο διάστημα
, τότε οι ρίζες βρίσκονται στο διάστημα ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) . Αυτό, γιατί
. Αυτό, γιατί  , (τιμές ομόσημες του συντελεστή του
, (τιμές ομόσημες του συντελεστή του  ), επομένως οι αριθμοί
), επομένως οι αριθμοί  βρίσκονται και οι δύο εκτός του διαστήματος
βρίσκονται και οι δύο εκτός του διαστήματος ![[y_1, y_2] [y_1, y_2]](/forum/ext/geomar/texintegr/latexrender/pictures/bf3fdda92a4e3bee74dcc437daf1ce45.png) των ριζών και
των ριζών και  γεγονός που αποκλείει να είναι και οι δύο αριθμοί
γεγονός που αποκλείει να είναι και οι δύο αριθμοί  αριστερότερα ή και οι δύο αριθμοί δεξιότερα του του διαστήματος
αριστερότερα ή και οι δύο αριθμοί δεξιότερα του του διαστήματος ![[y_1, y_2] [y_1, y_2]](/forum/ext/geomar/texintegr/latexrender/pictures/bf3fdda92a4e3bee74dcc437daf1ce45.png) .
. 
 , τότε οι ρίζες είναι τα
, τότε οι ρίζες είναι τα 

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες