 μια συνάρτηση για την οποία ισχύει
μια συνάρτηση για την οποία ισχύει  για κάθε
για κάθε  . Να βρείτε το
. Να βρείτε το  .
.Συντονιστής: m.pαpαgrigorakis
 μια συνάρτηση για την οποία ισχύει
μια συνάρτηση για την οποία ισχύει  για κάθε
για κάθε  . Να βρείτε το
. Να βρείτε το  .
.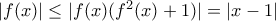 άρα
άρα 
 απο το κριτήριο παρεμβολής
απο το κριτήριο παρεμβολής 
Μπορώ να κάνω προσέγγιση με αντίστροφη;Christos.N έγραψε: ↑Τετ Απρ 08, 2020 3:13 pmακόμα πιο ισχυρή η συνέχεια
άρα
επειδήαπο το κριτήριο παρεμβολής

Από την δοθείσα έχουμε
 . Άρα το ζητούμενο όριο είναι
. Άρα το ζητούμενο όριο είναι  (άμεσο).
(άμεσο).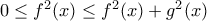 και
και  από κριτήριο παρεμβολής
από κριτήριο παρεμβολής 

 και
και 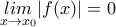 από το κριτήριο παρεμβολής
από το κριτήριο παρεμβολής 
Μπορείς να αποδείξεις ότι η αντίστροφη είναι συνεχής;
Βεβαίως και μπορείς, αλλά ίσως είναι εκτός ύλης: Εύκολα βλέπουμε ότι ηSilver έγραψε: ↑Τετ Απρ 08, 2020 3:16 pmΜπορώ να κάνω προσέγγιση με αντίστροφη;Christos.N έγραψε: ↑Τετ Απρ 08, 2020 3:13 pmακόμα πιο ισχυρή η συνέχεια
άρα
επειδήαπο το κριτήριο παρεμβολής

 είναι
είναι  και επί, οπότε η αντίστροφη υπάρχει. Θέτοντας όπου
και επί, οπότε η αντίστροφη υπάρχει. Θέτοντας όπου  το
το  βρίσκουμε
βρίσκουμε  και ειδικά
και ειδικά  . Έπεται ότι η αντίστροφη (και άρα η αρχική) είναι συνεχής. Το ζητούμενο όριο είναι (λόγω συνέχειας)
. Έπεται ότι η αντίστροφη (και άρα η αρχική) είναι συνεχής. Το ζητούμενο όριο είναι (λόγω συνέχειας)  .
.με χρώμα έχω σημειώσει αυτά που λέτε με αυτό το χρώμα .Mihalis_Lambrou έγραψε: ↑Τετ Απρ 08, 2020 3:30 pmΒεβαίως και μπορείς, αλλά ίσως είναι εκτός ύλης: Εύκολα βλέπουμε ότι ηSilver έγραψε: ↑Τετ Απρ 08, 2020 3:16 pmΜπορώ να κάνω προσέγγιση με αντίστροφη;Christos.N έγραψε: ↑Τετ Απρ 08, 2020 3:13 pmακόμα πιο ισχυρή η συνέχεια
άρα
επειδήαπο το κριτήριο παρεμβολής

είναι
και επί, οπότε η αντίστροφη υπάρχει. Θέτοντας όπου
το
βρίσκουμε
και ειδικά
. Έπεται ότι η αντίστροφη (και άρα η αρχική) είναι συνεχής. Το ζητούμενο όριο είναι (λόγω συνέχειας)
.
Και τι ακριβώς εννοείς; Ότι δεν είναι σωστό αυτό που γράφω;Christos.N έγραψε: ↑Τετ Απρ 08, 2020 3:38 pmμε χρώμα έχω σημειώσει αυτά που λέτε με αυτό το χρώμα .Mihalis_Lambrou έγραψε: ↑Τετ Απρ 08, 2020 3:30 pm
Βεβαίως και μπορείς, αλλά ίσως είναι εκτός ύλης: Εύκολα βλέπουμε ότι ηείναι
και επί, οπότε η αντίστροφη υπάρχει. Θέτοντας όπου
το
βρίσκουμε
και ειδικά
. Έπεται ότι η αντίστροφη (και άρα η αρχική) είναι συνεχής. Το ζητούμενο όριο είναι (λόγω συνέχειας)
.
 είναι επί του
είναι επί του  , μπορούμε εύκολα το μη φραγμένη.
, μπορούμε εύκολα το μη φραγμένη.Δεν διαφωνώ καθόλου. Όμως απαντώ στο Μαθηματικό μέρος του προβλήματος άσχετα αν είναι εντός ή εκτός ύλης ή πνεύματος (δεδομένου ότι το δήλωσα κιόλας). Οδηγός μου τα Μαθηματικά, χωρίς περιορισμούς.Christos.N έγραψε: ↑Τετ Απρ 08, 2020 3:54 pmΌπως γράφετε και εσείς,είναι εκτός ύλης για τον φάκελο, άλλο λάθος και άλλο εκτός πνεύματος σχολικού βιβλίου, διαφωνείτε;
 αντί
αντί  , δεν βλέπω άλλο πρόβλημα.
, δεν βλέπω άλλο πρόβλημα.Ουσιαστικά το έχω απαντήσει το αρχικό ποστ, αλλά ας γράψω λεπτομερέστερα έναν τέτοιο ήπιο τρόπο.Christos.N έγραψε: ↑Τετ Απρ 08, 2020 3:54 pmΠάντως εκεί που ακόμα το επεξεργάζομαι και έχω κάποια αμφιβολία είναι αν μπορούμε να δείξουμε (ήπια) ότι η συνάρτησηείναι επί του
, μπορούμε εύκολα το μη φραγμένη.
 πραγματικός. Επειδή η συνάρτηση
πραγματικός. Επειδή η συνάρτηση  είναι επί (απλό), υπάρχει
είναι επί (απλό), υπάρχει  με
με 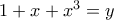 . Γι' αυτό το
. Γι' αυτό το  έχουμε
έχουμε 
Mihalis_Lambrou έγραψε: ↑Τετ Απρ 08, 2020 4:29 pmΟυσιαστικά το έχω απαντήσει το αρχικό ποστ, αλλά ας γράψω λεπτομερέστερα έναν τέτοιο ήπιο τρόπο.Christos.N έγραψε: ↑Τετ Απρ 08, 2020 3:54 pmΠάντως εκεί που ακόμα το επεξεργάζομαι και έχω κάποια αμφιβολία είναι αν μπορούμε να δείξουμε (ήπια) ότι η συνάρτησηείναι επί του
, μπορούμε εύκολα το μη φραγμένη.
Έστωπραγματικός. Επειδή η συνάρτηση
είναι επί (απλό), υπάρχει
με
. Γι' αυτό το
έχουμε

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες